Lista de probleme 28
Nivelul concursului: Național
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII Juniori
#2453
Rosii mici
Dan este un mare pasionat al fructelor, printre preferatele sale fiind strugurii şi pepenii. Însă recent şi-a descoperit și pasiunea pentru legume, în special pentru roşii, dar mai ales roşiile mici. Spre norocul lui, grădina bunicului este plină de roşii. Grădina are forma unei matrice cu N linii și M coloane cu elemente numere naturale, nu neapărat distincte, unde fiecare element din matrice reprezintă dimensiunea unei roşii. Matricea are proprietatea că oricare coloană are valorile ordonate crescător de sus în jos, adică de la prima spre ultima linie. Bunicul său îi cere să rezolve Q sarcini. Pentru fiecare sarcină, Dan primeşte un număr natural x şi trebuie să găsească o submatrice de arie maximă care începe de pe linia 1 a matricei care reprezintă grădina şi are toate elementele mai mici sau egale decât x. Pentru determinarea submatricei cerute, Dan are voie să mute toate valorile unei coloane în fața oricărei alte coloane. De asemenea, îi este permis să facă oricâte mutări de tipul acesta.
Să se calculeze aria maximă a unei submatrice care respectă specificațiile din enunț, pentru fiecare din cele Q sarcini date de către bunic.
ONI 2018 clasa a IX-a
- Fișiere
- Gemene Narcis Gabriel
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Căutare binară
- Cautare binara
#2454
bsrec
Fie un vector v sortat crescător cu N elemente naturale nenule distincte pe care nu le cunoaştem, dar pe care ne propunem să le determinăm. Având la dispoziţie acest vector v, cu ajutorul următorului algoritm de căutare binară putem răspunde la queryuri de forma: Dându-se un număr X şi un interval [a, b] se cere să se determine cel mai mic element mai mare decât X aflat în intervalul determinat de indicii a şi b, interval din vectorul v. Se cunosc paşii pe care algoritmul de cautare binară i-a urmat pentru diferite valori ale tripletului (X, a, b).
Dându-se N (lungimea vectorului), Q (numărul de query-uri apelate) şi cele Q query-uri, să se determine vectorul iniţial. Dacă există mai multe soluţii se va afişa soluţia minim lexicografică. Dacă nu există soluţie se va afişa valoarea -1.
ONI 2018 clasa a IX-a
- Fișiere
- Eugenie Daniel Posdărăscu
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Căutare binară
- Cautare binara
#2455
plaja2
Zizi îşi va petrece concediul în această vară într-o frumoasă staţiune de la Marea Neagră. Acolo va sta N zile. Zilele
sunt numerotate de la 1 la N. În fiecare dintre cele N zile de concediu, ea intenţionează să facă plajă un număr cât
mai mare de unităţi de timp. Va trebui să ţină seama totuşi de prognoza meteo, care este nefavorabilă în K dintre cele N zile, respectiv în zilele z[1], z[2], …, z[k]. În fiecare dintre aceste K zile va ploua sau va fi prea mult soare, iar Zizi va trebui să-şi limiteze timpii de plajă la cel mult t[1], t[2], …, t[k] unităţi de timp. De asemenea, din motive de confort fizic, Zizi doreşte ca diferenţa în valoare absolută a timpilor de plajă între oricare două zile consecutive să nu depăşească T.
Cunoscând zilele z[1], z[2], …, z[k] în care există limitările t[1], t[2], …, t[k] pentru timpul de plajă şi valoarea T, să se determine numărul maxim de unităţi de timp pe care Zizi le poate petrece la plajă într-o singură zi dintre cele N zile de concediu.
ONI 2018 clasa a IX-a
- Fișiere
- Constantin Gălățan
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Căutare binară
- Cautare binara
#2479
pietre
O tablă de joc cu n linii, numerotate de la 1 la n și m coloane, numerotate de la 1 la m conține n*m celule identice. Celula din colţul din stânga sus se află pe linia 1 şi coloana 1. O celulă poate fi: celulă liberă, celulă în care se află o piatră sau celulă de tip gaură.
Pietrele sunt numerotate cu valori începând de la 1. Numerotarea pietrelor pe tablă se face în ordinea în care sunt
date în fișierul de intrare. O celulă de pe tablă are maxim patru celule vecine, aflate în direcțiile: nord, vest, sud, est, iar o piatră poate sări doar peste o celulă vecină în care se află o piatră. În urma unei astfel de sărituri, piatra peste care s-a sărit dispare de pe tablă. Astfel, o piatră situată în celula de pe linia i și coloana j, poate sări :
- în direcția nord peste piatra situată în celula de pe linia
i-1și coloanajși ajunge în celula de pe liniai-2și coloanaj, iar piatra aflată pe liniai-1și coloanajdispare; o astfel de săritură se notează cu literaN; - în direcția est peste piatra situată în celula de pe linia
iși coloanaj+1și ajunge în celula de pe liniaiși coloanaj+2, iar piatra aflată pe liniaiși coloanaj+2dispare; o astfel de săritură se notează cu literaE; - în direcția sud peste piatra situată în celula de pe linia
i+1și coloanajși ajunge în celula de pe liniai+2și coloanaj, iar piatra aflată pe liniai+1și coloanajdispare; o astfel de săritură se notează cu literaS; - în direcția vest peste piatra situată în celula de pe linia
iși coloanaj-1și ajunge în celula de pe liniaiși coloanaj-2, iar piatra aflată pe liniaiși coloanaj-1dispare; o astfel de săritură se notează cu literaV.
O săritură a unei pietre este permisă doar dacă celula în care urmează să ajungă se află pe tabla de joc, este liberă și în celula peste care sare există o piatră.
Se cunoaște o succesiune de sărituri formată din maxim 255 de caractere S, N, E sau V, după care o piatră realizează săriturile specificate, în ordine, de la stânga la dreapta. Dacă piatra ar trebui execute o săritură care nu este permisă, poziţia ei nu se modifică şi se trece la săritura următoare din succesiune.
Să se determine numărul pietrei care efectuând sărituri în conformitate cu succesiunea dată, conduce la o configuraţie finală formată dintr-un număr minim de pietre pe tablă. Dacă există mai multe pietre care ar conduce la acelaşi număr minim de pietre în configuraţia finală, se va afişa valoarea cea mai mică dintre numerele de identificare ale pietrelor respective.
ONIgim2018
- Fișiere
- Tîmplaru Roxana
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#2497
gene
Gigel este curios să afle în ce zonă a țării au trăit cei mai mulți dintre strămoșii săi. El reușește să adune informații despre structura genetică a persoanelor din diferite părți ale țării și speră că, prin compararea cu propria structură genetică, să identifice o zonă pătratică în care au trăit cei mai mulți dintre strămoșii săi.
Structura genetică a unei persoane este reprezentată sub forma unei secvențe cu cel mult 20 de caractere (litere mici ale alfabetului englez). O persoană poate fi considerată strămoș a lui Gigel dacă gradul de similaritate dintre secvența corespunzătoare persoanei respective și cea a lui Gigel este mai mare strict decât un număr K, cunoscut.
Gradul de similaritate dintre două secvențe este reprezentat de numărul de caractere comune celor două secvențe. De exemplu pentru secvențele abcdabd și acbdaad gradul de similaritate este 6 (2 caractere a, 2 caractere d, 1 caracter b, 1 caracter c).
Gigel reprezintă harta țării sub forma unui tablou bidimensional cu N linii și M coloane în care fiecare element reprezintă structura genetică a unei persoane din zona respectivă.
Cunoscând N , M , K , structura genetică pentru Gigel și reprezentarea hărții identificată de acesta, să se determine:
1) poziția pe hartă și structura genetică pentru persoana, sau persoanele, pentru care gradul de similaritate cu structura genetică a lui Gigel este maxim;
2) o zonă pătratică, de dimensiune maximă în care toate persoanele ar putea fi strămoși ai lui Gigel.
ONIG 2018
- Fișiere
- Raluca Costineanu
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#2505
jocxzero
Pe o foaie dintr-un caiet de matematică de dimensiune N x M (N numărul de linii și M numărul de coloane) sunt completate toate pătrățelele cu X sau 0. Pentru un număr natural K dat, numim șir corect, o secvență de K elemente consecutive pe linie, coloană sau diagonale care au aceeași valoare (X sau 0). Două pătrățele de pe foaie sunt vecine pe aceeași diagonală dacă au un singur colț comun.
Exemplu din figura alăturată, pentru care N=4, M=5, K=3 conține 6 șiruri corecte de X și 5 șiruri corecte de 0.
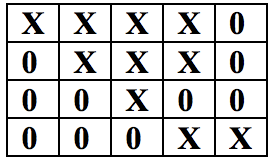
Cerințe:
- Se dau numerele naturale
N,MșiKși o foaie de matematică plină cuXși0. Determinați câte șiruri corecte deXși câte șiruri corecte de0se găsesc pe foaia dată. - Se dau
Qîntrebări de formaA B, în careAeste caracterulXsau0șiBeste un număr natural. Determinați în câte moduri putem tăia foaia de matematica vertical pentru a obține în subtabloul din partea stângă exactBșiruri corecte deA. Foia se poate tăia înM -1variante: după prima coloană, a doua coloană, după a treia coloană, ș.a.m.d, până după penultima coloană.
ONIG 2018
- Fișiere
- Octavian Dumitrascu
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#2451
mexitate
Se dă o matrice A cu N linii și M coloane cu elemente numere naturale nu neapărat distincte. Pentru o submatrice definim mex-ul acesteia ca fiind cea mai mică valoare naturală nenulă care nu apare în aceasta.
Să se calculeze produsul mex-urilor tuturor submatricelor având K linii și L coloane ale matricei A.
ONI 2018 clasa a IX-a
- Fișiere
- Eugenie Daniel Posdarascu
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Parcurgerea matricelor oarecare
- Vector de frecvență
#2625
viitor
Stațiunea Xoni de pe insula Ixos are N magazine de înghețată, așezate unul lângă altul, pe aceeași parte a străzii pietonale. Acestea sunt numerotate cu valori naturale de la 1 la N , în ordinea așezării pe stradă.
Magazinele sunt deținute de K acționari (numerotați de la 1 la K ), fiecare dintre aceștia fiind proprietarul unor magazine numerotate consecutiv. Un magazin poate avea mai mulți acționari.
Odată cu venirea verii, începe și perioada concediilor, toți acționarii luându-și concediul împreună, timp de M zile. Înainte de a pleca în concediu, ei au discutat cu Transportel pentru a se ocupa de aprovizionarea cu înghețată a magazinelor lor. Acesta a decis, singur, să facă în fiecare dintre cele M zile aprovizionarea unor magazine, numerotate și acestea cu numere consecutive.
Determinați, pentru fiecare acționar numărul de magazine deținute de către acesta care nu au fost aprovizionate cu înghețată în nicio zi din concediu.
ONIgim 2018
- Fișiere
- Marius Nicoli
- concurs
- Clasa 9 Probleme diverse Probleme diverse
- Cautare binara
#2570
mostenire
Regele Rufus dorește să stabilească moștenitorul averii sale, adică să ofere parola de la seif celui mai deștept dintre fiii săi. Inițial, regele a avut parola X formată din N cifre nenule și un cod cheie Q (număr natural cu exact nouă cifre, distincte, toate nenule). În fiecare an din cei K ani de domnie, folosind codul cheie Q, Rufus a modificat câte o secvență de cifre din parolă ajungând la parola finală P.Pentru fiecare secvență se cunoaște poziția S a primei cifre din secvență și poziția D a ultimei cifre din secvență. Astfel, secvența este formată din cifrele situate pe pozițiile S, S+1, S+2,…, D în parola X.
Modificarea unei secvențe din X constă în înlocuirea fiecărei apariții a cifrei 1 cu prima cifră a lui Q, apoi a fiecărei apariții a cifrei 2 cu a doua cifră a lui Q,…, a fiecărei apariții a cifrei 9 cu ultima cifră a lui Q.
Pentru a decide moștenitorul, regele le dă fiilor parola finală P, codul cheie Q, numărul K de ani de domnie și cele K secvențe de cifre care au fost modificate și le cere să găsească: parola inițială X, poziția minimă Z din parola X care a apărut în cele mai multe secvențe dintre cele modificate de rege de-a lungul celor K ani de domnie și cifrele distincte care au ocupat poziția Z în cei K ani.
Scrieți un program care citește numerele Q, N, K, cele N cifre ale parolei finale P și cele K perechi de poziții S și D, și care rezolvă următoarele două cerințe:
- determină parola inițială
X; - determină poziția minimă
Zși cifrele distincte care au ocupat această poziție în ceiKani de domnie.
ONIG 2018
- Fișiere
- Flavius Boian
- concurs
- Clasa 9 Probleme diverse Probleme diverse
- Vector de frecvență
#2472
fractal
Andra este o fetiță pasionată de desen. Pentru a-și îmbunătăți performanțele școlare la geometrie, Andra îmbină pasiunea pentru desen cu rezolvarea problemelor de geometrie. Astfel, pe o foaie de matematică împărțită în pătrățele dispuse pe \(2^N \) linii şi \(2^N \) coloane, Andra desenează în centru o figură de forma unui pătrat de latură \(2^{N-1} \) (figura 1) . Pentru fiecare colț al figurii, Andra desenează alte 4 noi figuri cu latura egală cu jumătate din latura figurii inițiale (Figura 2). Repetă procedeul de desenare pentru fiecare nouă figură obținută, până când ajunge la marginea foii de hârtie, fără a depăși marginile acesteia. Fiecare pătrățel care face parte dintr-o figură desenată este colorat, pentru a se distinge pe foaia de hârtie. Fiecare figură desenată este un pătrat cu laturile paralele cu marginile foii de hârtie.
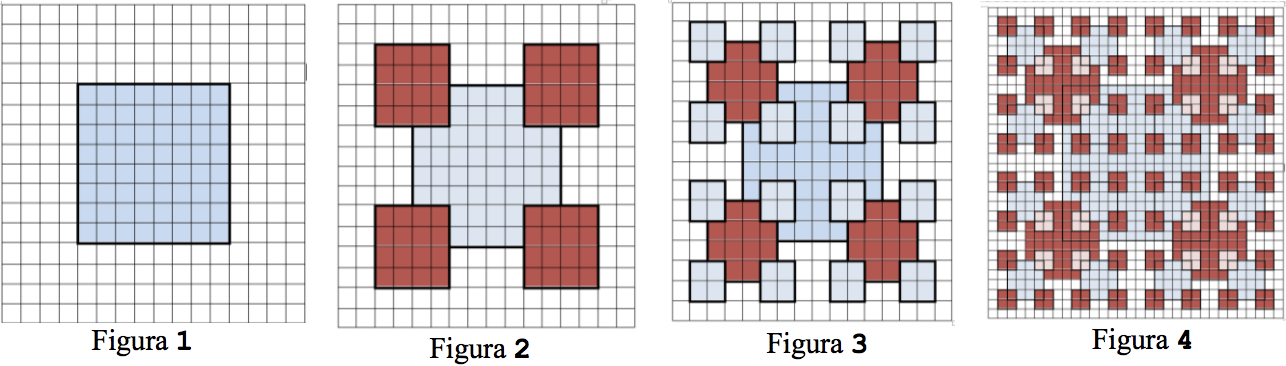
Scrieţi un program care citește numărul N , corespunzător dimensiunii de \(2^N\) x \(2^N \) a foii de desen şi determină:
1) Numărul de figuri de latură minimă desenate;
2) Numărul total de pătrățele colorate cel puțin o dată de pe foaia de hârtie.
Baraj ONIG 2018
- Fișiere
- Cardas Cerasela Daniela
- concurs
- Clasa 9 Probleme diverse Probleme diverse