Lista de probleme 39

Vasilică vizitează cetățile medievale. Fiind curios, el încearcă să descopere pasajele secrete și ascunzătorile. Din nefericire, s-a rătăcit și a ajuns într-o sală din care nu poate ieși decât trecând printr-un labirint. Există o hartă a labirintului, o matrice de n linii și m coloane, un element din această matrice reprezentând o cameră. Deplasarea în labirint se poate face numai prin camerele adiacente pe orizontală și verticală. Intrările în labirint sunt notate cu A, ieșirile cu C, iar camerele zidite (inaccesibile) cu Z. Ieșirea din labirint se poate face din una din camerele C, în fiecare astfel de cameră existând câte un elicopter încuiat. Toate elicopterele se deschid cu aceeași cheie, câte un exemplar al cheii aflându-se în camerele B. Trecerea în altă cameră va dura 1 unitate de timp. Pentru a ieși din labirint Vasilică intră pe una din intrările notate cu A, ia cheia dintr-o cameră B și iese din labirint printr-o cameră C. El va intra în camera A la timpul 1. Camerele de tip A pot fi situate oriunde pe hartă. În drumul de la o cameră de tip A către o cameră de tip B se poate trece printr-o cameră de tip C fără a se ieși din labirint. Ajutați-l pe Vasilică să iasă cât mai repede din labirint.

Un labirint este descris ca fiind o matrice binară cu N linii și M coloane, cu semnificația că 0 reprezintă o poziție liberă, iar 1 reprezintă o poziție în care se află un zid. Un drum în labirint este un traseu în matrice care începe cu poziția (1, 1) și ajunge în poziția (N, M) prin deplasare doar pe poziții care au valoarea 0 și sunt vecine cu poziția curentă, pe una din cele patru direcții: sus, jos, stânga, dreapta. Lungimea unui drum este egală cu numărul de poziții vizitate. Notăm cu d0 lungimea drumului minim de la poziția (1, 1) la poziția (N,M). Fie d(i, j) lungimea drumului minim de la poziția (1, 1) la poziția (N, M), dacă poziției (i, j) i se atribuie valoarea 0. Observăm că dacă poziția (i, j) conține inițial un 0, atunci d0 = d(i, j). Pentru fiecare poziție (i, j) să se verifice dacă d(i, j) < d0.

Data stelară 3210: Căpitanul navei USS Entrerprise, Jean-Luc Picard se află într-o misiune importantă în cuadrantul Beta al galaxiei. Acesta trebuie să ajungă cât mai rapid de la planeta Vulcan până la planeta Qo’noS, dar din păcate pentru această misiune Jean-Luc Picard nu va putea să ajungă instantaneu la destinație folosind warp drive-ul navei, ci va trebui să se deplaseze în mod normal, din sector în sector. Vouă vă revine rolul de a îl ajuta pe Jean-Luc Picard și să îi răspundeți la una din următoarele întrebări știind harta galaxiei:
- Care este numărul maxim de sectoare ale galaxiei Smax afectate la orice moment de timp de către cel puțin un pulsar.
- Care este timpul minim Tmin de care are nevoie Jean-Luc Picard pentru a ajunge pe planeta Qo’noS.

Cunoscându-se N și M, dimensiunile satului, C numărul cailor, forțele inițiale ale cailor și matricile a și p, să se determine numărul de cai pe care Lică îi poate utiliza astfel încât el să reușească să traverseze satul, de la casa lui până la ieșirea din sat.

Adrian și-a luat un elicopter. Evident, un elicopter de jucărie. Adrian se joacă cu elicopterul său pe o suprafață reprezentată de o matrice de n×m, unde se află turnuri. Fiecare turn se află în celula reprezentată de indicii i și j, având înălțimea h[i][j]. În jocul său, Adrian dorește să piloteze elicopterul său. Inițial, elicopterul este ridicat în aer la o anumită înălțime, și poziționat într-o celulă aflată pe prima coloană. Pe parcursul jocului, elicopterul este menținut la înălțimea inițială. La fiecare pas, elicopterul se poate muta în una din celulele învecinate pe linie sau pe coloană, în stânga, dreapta, sus sau jos, doar dacă înălțimea turnului nu este mai mare decât înălțimea la care se află elicopterul. Jocul se termină când elicopterul ajunge într-o celulă aflată pe ultima coloană.

Să se determine cea mai mică valoare a înălțimii la care trebuie ridicat elicopterul, astfel încât acesta să poată ajunge pe o celulă aflată pe ultima coloană.

Dealul Bucium este cunoscut pentru tradiția de sute de ani a cultivării viței de vie. Acolo au fost plantați demult butuci de vie de soi nobil și de soi hibrid, pe un teren de formă dreptunghiulară. Din păcate, în anii ploioși, via este atacată de o boală fungică numită plasmopara, care afectează doar soiurile hibride. În fiecare nouă zi ploioasă, plasmopara atacă butucii învecinați (la nord, est, sud și vest) cu butuci deja infectați. Butucii atacați în prima zi ploioasă sunt cei din colțurile terenului, fiind cei mai expuși. Cunoscând numărul de rânduri de viță de vie și numărul de butuci de pe fiecare rând, cunoscând numărul de zile ploioase și dispunerea soiurilor pe teren, să se determine:
1. numărul butucilor de soi hibrid care au rămas neafectați de plasmopara
2. ziua în care au fost afectați cei mai mulți butuci (dacă niciun butuc nu a fost afectat, rezultatul va fi 0; dacă sunt mai multe zile cu număr maxim de butuci afectați, se va determina prima dintre acestea).

În arhipelagul X, ajunge un peşte de aur. După drumul obositor parcurs de peşte, el vrea să se relaxeze într-o anumită zonă din acest arhipelag (cu coordonatele x2, y2). Totodată, acest peşte este curios să afle câte modalităţi sunt ca să ajungă în acea zonă.

Se dă o matrice cu n linii și m coloane. Pentru k poziții date, se cere să se determine drumul de lungime minimă care pleacă de la poziția i1 și j1 și trece prin toate cele k poziții (nu contează în ce ordine), ajungând în final în poziția i2 si j2.

Cârtițele sunt animale de dimensiuni mici care își duc traiul pe suprafețe de teren deschis, având ca dușman principal vulpea. Lângă o pădure se află o zonă agricolă în forma dreptunghiulară, împărțită în pătrățele de aceeași dimensiune. Zona agricolă este reprezentată printr-un tablou bidimensional cu M linii și N coloane, având liniile și coloanele numerotate începând cu 1. În aceasta zona agricolă trăiește o cârtiță și K vulpi.

Pentru cârtiță cunoaștem coordonatele ei (linia și coloana) pe care se găsește, la fel și pentru vulpi, care stau la pânda pentru a ataca cârtita în momentele ei de neatenție.
Pe suprafața terenului cârtita se poate deplasa din pătrățelul în care se afla doar într-unul dintre cele 4 pătrățele vecine pe direcțiile nord, sud, est sau vest.
Vulpile pot ataca instantaneu pe o raza de acțiune de lungime 0, 1 sau 2 pe orizontala și verticala, inclusiv în poziția unde se găsesc, după care tot instantaneu se întorc în pozițiile inițiale. În figura de mai jos sunt desenate pătrățele unde poate ataca o vulpe poziționață în pătrățelul cu cifra reprezentând raza de acțiune.

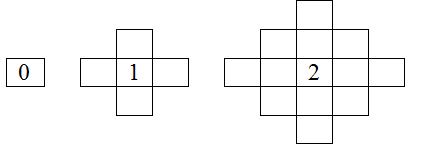
Pentru a micșora riscul de deplasare în zona agricolă cârtița sapă în pământ un sistem de G galerii, care leagă între ele pătrățele din zona agricola. Aceste galerii nu se intersectează sub pământ, ci doar la suprafață, trecerea dintr-o galerie în alta, care se intersectează în același pătrățel făcându-se printr-un sistem ce nu îi pune viata în pericol. Galeriile sunt indicate prin coordonatele pătrățelelor pe care le unesc. Acestea sunt săpate astfel încât, dacă pornim dintr-un capăt al unei galerii le putem parcurge pe toate. Nu exista doua galerii care sa pornească din același pătrățel și să ajungă tot în același pătrățel (galeriile sunt distincte).

Cârtița dorește sa se plimbe prin toate galeriile de sub teren trecând o singura data prin fiecare, dar pentru acest lucru trebuie sa ajungă nevătămată mergând la suprafața terenului la un pătrățel de unde să intre în sistemul de galerii.

Determinați:

1. cel mai apropiat pătrățel de poziția inițială a cârtitei prin care ea poate să intre în galerie pentru a se plimba, precum și lungimea traseului parcurs la suprafață astfel încât fiecare pătrățel de pe traseu sa nu fie atacat de nicio vulpe;
2. traseul de plimbare numai prin galerii, specificat prin coordonatele pătrățelelor care constituie capetelor acestora.