Lista de probleme 36
Filtrare
#112
FractieMinima
Să se scrie un program care citește un șir de n numere naturale şi determină cea mai mică fracţie care poate fi scrisă cu numărătorul şi numitorul dintre cele n numere.
- Consola
- Silviu Candale
- medie
- Clasa 9 Algoritmi elementari Divizibilitate
- Algoritmul lui Euclid
- Maxime și minime
#410
Cmmdc2
Se citește un număr natural n. Acest număr se “împarte” în alte două numere a și b, astfel: a este format din cifrele din prima jumătate a lui n, b este format din cifrele din a doua jumătate a lui n. Dacă n are număr impar de cifre, cifra din mijloc se ignoră. De exemplu, dacă n=9183792, atunci a=918, iar b=792. Să se determine cel mai mare divizor comun al lui a și b.
#390
SPFractii
Se dau 4 numere naturale a b c d, reprezentând fracțiile \(\frac{a}{b}\) și \(\frac{c}{d}\). Calculați suma și produsul celor două fracții, aduse la forma ireductibilă.
- Consola
- Silviu Candale
- ușoară
- Clasa 9 Algoritmi elementari Divizibilitate
- Algoritmul lui Euclid
#391
Fractii
Se dau n perechi de numere naturale, nenule, fiecare reprezentând câte o fracţie. Calculaţi suma celor n fracţii, aducând rezultatul la forma ireductibilă.
- Consola
- Silviu Candale
- ușoară
- Clasa 9 Algoritmi elementari Divizibilitate
- Algoritmul lui Euclid
#3307
fractie6
Se dă un numar n și n perechi de numere naturale a și b.Să se determine dacă a/b este fracție finită sau periodică, iar dacă este fracție periodică să se determine dacă este fracție periodică simplă sau mixtă.
- Consola
- Traian Florian Alin Moldoveanu
- ușoară
- Clasa 9 Algoritmi elementari Divizibilitate
- Divizibilitate
- Algoritmul lui Euclid
- Cmmdc
#305
CmmdcN
Se dau n numere naturale nenule. Calculaţi cel mai mare divizor comun al lor.
#378
Pavare
Curtea bunicului este de formă dreptunghiulare cu dimensiunile cunoscute. Bunicul dorește pavarea curții cu plăci de piatră. Firma furnizoare produce plăci de piatră de formă pătrată, de orice dimensiune, iar bunicul dorește să folosească plăci de o singură dimensiune, astfel încât să folosească cât mai puține plăci. NU este posibilă tăierea plăcilor de piatră, iar curtea trebuie pavată în întregime.
Cunoscând dimensiunile curții, determinați numărul minim de plăci cu care poate fi pavată curtea și dimensiunea acestora.
- Consola
- Silviu Candale
- ușoară
- Clasa 9 Algoritmi elementari Divizibilitate
- Algoritmul lui Euclid
#3486
FactorulX
Numim factorul-x a 2 numere produsul tuturor factorilor primi comuni și diferiți ai celor 2 numere.
Se dau n numere naturale distincte. Se cere să se afle câți factori-x diferiți pot fi obținuți din toate perechile diferite de numere din șir și să se afișeze aceștia.
- Fișiere
- Alexandru Lorintz
- medie
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
- Divizibilitate
- Algoritmul lui Euclid
- Cautare binara
- Descompunere in factori
#2611
raza
Avem la dispoziție un chenar dreptunghiular format din oglinzi. O rază de lumină pornește din colțul stânga jos al dreptunghiului sub un unghi de 45 de grade față de latura de jos a dreptunghiului și lovește latura de sus sau latura din dreapta. Aici se reflectă (pornește spre o altă latură tot sub un unghi de 45 de grade față de latura de care s-a lovit). Își continuă drumul până când ajunge într-un colț al dreptunghiului.
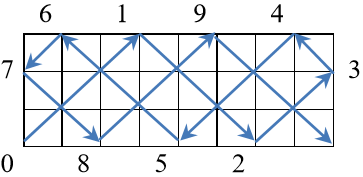
Admitere UBB-Cluj 2017
- Consola
- Nicoli Marius
- concurs
- Clasa 9 Algoritmi elementari Divizibilitate
- Algoritmul lui Euclid
#2748
patrula3
Un domeniu pătrat (cu albastru), ca cel din figură trebuie apărat. Domeniul e împărțit în pătrățele. Latura domeniului este de n pătrățele, n≥7. Pe culoarele colorate patrulează 3 soldați, care încep patrularea din colțul stânga sus în același moment (poziția inițială). În exemplul de mai jos avem n=9.
Cei 3 soldați (garda) se vor schimba cu alți 3 soldați în momentul în care ajung în poziția inițială, simultan.
Soldații patrulează în sensul acelor de ceasornic fiecare cu aceeași viteză constantă, și fiecare pe culoarul său.
Să se scrie un program care determină numărul de circuite complete pentru fiecare soldat (un circuit complet este făcut de un soldat oarecare, pe același culoar până ajunge în poziția inițială), pentru schimbarea gărzii.
S1 patrulează pe culoarul galben, S2 pe gri, S3 pe roșu. Albastrul este cetatea care trebuie apărată.
Pregatire UBB
- Consola
- -
- medie
- Clasa 9 Algoritmi elementari Divizibilitate
- Algoritmul lui Euclid