Lista de probleme 5

În antrenamentul său intens pentru prinderea lui Daffy Duck, celebrul vânător Elmer Fudd a început să vâneze rațe în orașul său preferat, Craiova. Se știe că există N rațe reprezentate prin puncte în planul de coordonate xOy, având coordonatele (x,y) și M ziduri sub forma unor segmente verticale având un capăt pe axa Ox și o anumită înălţime fiecare.

Vânătorul Elmer dorește să împuște cât mai multe rațe. El poate fi poziționat în orice punct de abscisă număr natural nenul, pe axa Ox. O rață poate fi ochită de vânător dacă zidul nu blochează glonțul vânătorului, adică segmentul imaginar delimitat de rață și de vânător nu se intersectează cu nici un zid.

Să se afle numărul maxim de rațe care pot fi ochite de vânătorul Elmer.

XORin este nemulțumit de problemele primite în prima zi de concurs de la Olimpiada Națională de Informatică și decide astfel să se implice în comisie. În scurt timp devine specialistul comisiei în generarea de teste formate din șiruri de numere. Din când în când el trebuie să adauge sau să șteargă elemente din șir. Câteodată el decide să readauge dintre elemente șterse anterior. Fie șirul de numere a=(a[1], a[2], … ,a[N]) și N numărul de elemente din șir după fiecare operație.

Astfel el are de realizat următoarele operații pornind de la un șir vid:

• Inserează la sfârșitul șirului o valoare x;
• Șterge ultimele x elemente din șir;
• Readaugă la sfârșitul șirului primele x elemente șterse. Dacă, de exemplu, în operația anterioară de ștergere a unui număr y de elemente, am șters elementele a[N-y+1], a[N-y+2],…, a[N], iar acum urmează o operație de readăugare a x elemente, vor fi adăugate în ordine elementele a[N-y+1], a[N-y+2],…, a[N-y+x] la sfârșitul șirului.

Din când în când XORin își pune următoarea întrebare: de câte ori există valoarea x în șir?

La un concurs de informatică participă 2∙N elevi împărțiți în N echipe de câte 2. Echipa poate lucra în comun la problemele propuse doar dacă au calculatoarele în rețea. Laboratorul de informatică este unul special: are 2∙N calculatoare, distribuite pe două rânduri la distanță de un metru între ele (vertical și orizontal) și N cabluri de rețea de lungime un metru. Concursul se desfășoară pe mai multe zile și nu există două zile de concurs cu aceeași configurație a rețelei.

Exemplu: pentru N=3, cei 6 elevi au fost împărțiți în 3 echipe, iar aranjarea rețelei în cele 3 zile de concurs este cea din figura de mai jos.

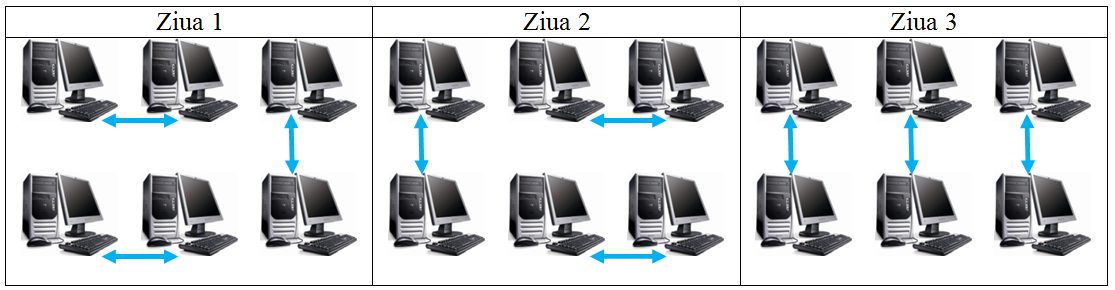
Administratorul laboratorului vrea să memoreze în ordine lexicografică toate configurațiile folosite în zilele de concurs. Cablul orizontal se notează prin 0, iar cel vertical prin 1. Lucrând ordonat și eficient, pentru cele trei zile el își va nota valorile: 001, 100, respectiv 111. Se observă că o reprezentare de genul 000, 010, 011, 101 nu poate fi realizată.

Cunoscând N, să se determine:

1. Numărul de zile modulo 1000000007 în care se desfășoară concursul.
2. Configurațiile laboratorului în ziua X-1 și ziua X+1, cunoscând configurația zilei X.

Pentru că s-a calificat la Olimpiada Națională de Informatică de la Craiova, NN îi pregătește lui XORin un tort. Tortul este dreptunghiular, format din linii și coloane numerotate de la 1 la N pentru linii și de la 1 la M pentru coloane. Tortul este format din bucăți de dimensiune 1x1, fiecare fiind acoperită cu un alt tip de glazură. În fiecare zi NN îi taie lui XORin câte o felie, alegând cel mai mare pătrat care conține bucăți acoperite cu același tip de glazură. În cazul în care există mai multe astfel de felii, NN o alege pe cea care are colțul din dreapta jos situat pe linia cu indicele cel mai mic. Dacă și în acest caz există mai multe posibilități, el o va alege pe cea cu colțul din dreapta jos situat în coloana cu indicele cel mai mic.

Precizați latura și coordonatele colțului din dreapta jos pentru fiecare felie de tort primită, în ordinea specificată mai sus.

Se consideră două șiruri de caractere A și B, ambele șiruri având același număr de caractere.

Asupra șirurilor se aplică următorul algoritm:

• șirul A se permută circular cu ki poziții spre stânga
• din cele două șiruri se elimină caracterele care coincid din punct de vedere al poziției și valorilor

Algoritmul se oprește când fie ambele șiruri devin vide, fie șirurile nu mai au caractere comune. Valoarea ki pentru fiecare pas i reprezintă al i-lea număr prim din mulțimea numerelor prime.

Dându-se N și M, să se genereze șirurile A și B, ambele având lungimea N, astfel încât numărul de repetări ale algoritmului aplicat celor două șiruri să fie M.