Lista de probleme 14
Nivelul concursului: Județean
http://olimpiada.info/oji2011/
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII
#1073
Numerus
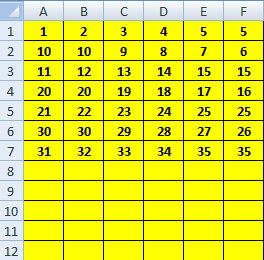 La ora de matematică distractivă, domnul profesor Numerus propune elevilor săi să completeze cu numere naturale o grilă cu
La ora de matematică distractivă, domnul profesor Numerus propune elevilor săi să completeze cu numere naturale o grilă cu 6 coloane numerotate cu literele A, B, C, D, E şi F şi cu un număr infinit de linii. Grila va fi completată cu numere naturale, începând cu numărul 1. Pe liniile impare completarea se va face de la stânga la dreapta, iar pe cele pare de la dreapta la stânga. Ultimul număr de pe o linie va fi identic cu penultimul număr (în sensul completării) de pe aceeaşi linie.
În figura alăturată aveţi completate primele 7 linii ale grilei.
Deoarece pe tablă sau pe o foaie de hârtie numărul de linii este limitat, deci grila poate fi efectiv completată doar pentru un număr mic de linii, domnul profesor Numerus doreşte ca elevii săi să determine, cu ajutorul calculatorului, imaginea unei anumite linii a grilei şi locul sau locurile pe care se poate afla un număr natural dat.
Deduceţi regula după care se completează linia k a grilei şi scrieţi un program care să citească numerele naturale k şi n şi care să determine:
a) numerele naturale de pe linia k, vizualizate de la stânga la dreapta;
b) linia pe care se află în grilă numărul natural n;
c) coloana sau coloanele pe care se află în grilă numărul natural n.
OJI 2011, Clasa a V-a
- Fișiere
- Ana Intuneric
- concurs
- Clasa 9 Algoritmi elementari Probleme diverse
#1076
Grupe
Se consideră un tablou bidimensional cu m linii, n coloane şi elemente numere naturale. Pentru fiecare element se determină numărul de divizori pozitivi. Se formează apoi grupe cu elementele tabloului care au acelaşi număr de divizori, grupe notate G1, G2, …, Gk. Se ordonează descrescător grupele după numărul de elemente ce le conţin. Se ştie că o grupă G1 se află în faţa unei alte grupe G2 dacă G1 are mai multe elemente decât G2 sau, în cazul în care cele două grupe conţin acelaşi număr de elemente, numărul de divizori ai elementelor din grupa G1 este mai mare decât numărul de divizori ai elementelor din grupa G2. După ordonarea descrescătoare a grupelor, notăm prima grupă cu A şi a doua grupă cu B. În cazul în care toate elementele vor avea acelaşi număr de divizori, va exista o singură grupă, grupa A.
Scrieţi un program care citeşte m, n, elementele tabloului şi afişează:
a) numărul de divizori pozitivi pentru grupa A, numărul de elemente din grupă şi cea mai mare valoare din grupă;
b) numărul de divizori pozitivi pentru grupa B, numărul de elemente din grupă şi cea mai mare valoare din grupă; în cazul în care nu există grupa a doua, se va afişa de trei ori valoarea 0.
OJI 2011, Clasa a VII-a
- Fișiere
- Roxana Timplaru
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#1064
Cri
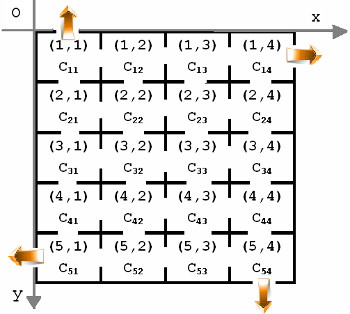 Furnicuţa şi-a construit un depozit pentru grăunţe pe o suprafaţă de teren dreptunghiulară şi l-a compartimentat în
Furnicuţa şi-a construit un depozit pentru grăunţe pe o suprafaţă de teren dreptunghiulară şi l-a compartimentat în N*M camere identice, de formă pătratică, dispuse câte M pe direcţia Ox şi câte N pe direcţia Oy. Din fiecare cameră se poate intra în orice cameră învecinată cu ea (cameră care are un perete comun cu aceasta).
În fiecare cameră, identificată prin coordonatele sale, ca în desenul alăturat în care N=5 şi M=4, furnica a depozitat o cantitate de grăunţe. De exemplu, în camera de coordonate (I,J) este depozitată cantitatea CIJ de grăunţe.
Atât intrarea cât şi ieşirea din depozit se poate face doar prin cele patru camere din colţurile depozitului, adică cele de coordonate (1,1), (1,M), (N,1) şi (N,M) care comunică cu exteriorul.
Pentru a asigura circulaţia aerului în depozit, furnica a montat un sistem de ventilaţie în camera de coordonate (X,Y).
Văzând ce multe grăunţe are furnica pentru iarnă, vecinul ei, leneşul greieraş Cri, s-a hotărât să fure din ele.
Cri s-a gândit să intre în depozit prin sistemul de ventilaţie din camera de coordonate (X,Y) şi să iasă prin una din cele 4 camere din colţurile depozitului care comunică cu exteriorul.
A studiat planul depozitului şi a împărţit camerele în patru zone:
- prima zonă, numerotată cu
1, conţine toate camerele de coordonate(I,J)cu1 ≤ I ≤ Xşi1 ≤ J ≤ Y, cu ieşirea prin camera de coordonate(1,1) - a doua zonă, numerotată cu
2, conţine toate camerele de coordonate(I,J)cu1 ≤ I ≤ XşiY ≤ J ≤ M, cu ieşirea prin camera de coordonate(1,M) - a treia zonă, numerotată cu
3, conţine toate camerele de coordonate(I,J)cuX ≤ I ≤ Nşi1 ≤ J ≤ Y, cu ieşirea prin camera de coordonate(N,1) - a patra zonă, numerotată cu
4, conţine toate camerele de coordonate(I,J)cuX ≤ I ≤ NşiY ≤ J ≤ M, cu ieşirea prin camera de coordonate(N,M)
Cri va intra doar într-una din cele patru zone şi va fura grăunţele doar din camerele conţinute de zona aleasă. Pentru a nu declanşa alarma furnicuţei, el va trebui să treacă cel mult o dată prin fiecare cameră din zonă, să fure întreaga cantitate de grăunţe din aceasta şi să iasă din depozit prin camera ce comunică cu exteriorul, corespunzătoare zonei alese.
Cri va trebui să aleagă zona în care va intra astfel încât cantitatea totală T de grăunţe furate să fie maximă, iar numărul K de camere prin care va trece să fie minim.
Scrieţi un program care să determine numerele naturale Z, T şi K, unde Z reprezintă numărul zonei pe care va trebui s-o aleagă Cri astfel încât cantitatea totală T de grăunţe furate să fie maximă, iar numărul K de camere prin va trece să fie minim.
OJI 2011, Clasa a IX-a
- Fișiere
- Carmen Minca
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
#1074
Carte
Rareş a primit în dar o carte în care paginile sunt amestecate. Se hotărăşte totuşi să o citească, răsfoind cartea într-un singur sens, de la prima pagină către ultima, în ordinea aşezării lor în carte, respectând următorul algoritm:
Caută la început pagina numerotată cu x=1.
După ce a citit pagina cu numărul x caută printre paginile următoare acestei pagini, răsfoind cartea, pagina cu numărul x+1, fără a căuta printre paginile aşezate înaintea paginii cu numărul x. Dacă o găseşte atunci va continua lectura în acelaşi mod, iar dacă nu o găseşte atunci va închide cartea şi, în ziua următoare, va relua lectura de la pagina cu numărul x+1, pe care mai întâi o va caută răsfoind cartea de la început.
Rareş va proceda la fel şi în zilele următoare până când va citi întreaga carte.
Scrieţi un program care citeşte un număr natural n, reprezentând numărul paginilor din carte şi n numere naturale distincte x1, x2,…, xn, reprezentând ordinea în care sunt aşezate cele n pagini în carte, şi care determină:
a) numărul zilelor în care Rareş citeşte cartea;
b) prima zi în care Rareş a citit cele mai multe pagini şi numărul paginilor citite în acea zi.
OJI 2011, Clasa a VI-a
- Fișiere
- Cristina Sichim
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Parcurgerea vectorilor
#1072
Magic
Rămaşi singuri în pădure, Hansel şi Grettel, ştiu că singura lor şansă de supravieţuire este să găsească şi să intre în Castelul de Turtă Dulce. Poarta castelului este închisă şi pentru a intra este nevoie de un cuvânt magic şi de un număr fermecat.
Zâna cea Bună îi vede pe copii şi pentru că vrea să–i ajute le spune:
„Mergeţi tot înainte, iar în drumul vostru o să întâlniţi copaci pe a căror trunchiuri sunt scrise caractere reprezentând litere sau cifre. Cuvântul magic este format din toate caracterele literă în ordinea în care apar, dar scrise toate cu majuscule. Numărul fermecat este cel mai mic număr cu cifre distincte care se poate forma din caracterele cifră.”
Pentru a-i ajuta pe Hansel şi Grettel să intre în Castelul de Turtă Dulce, scrieţi un program care citeşte un număr natural n, apoi n caractere şi determină:
a) cuvântul magic;
b) numărul fermecat;
OJI 2011, Clasa a V-a
- Fișiere
- Suzana Galatan
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
#1075
Grad1
Se consideră un şir x1, x2, …, xn de n numere naturale distincte, două câte două. Pentru o secvenţă de k numere (xp, xp+1, ..., xp+k-1), care începe cu numărul de pe poziţia p din şirul dat, definim gradul său ca fiind numărul de numere din secvenţă, care rămân pe aceleaşi poziţii după ordonarea crescătoare a secvenţei. De exemplu, pentru n=7 şi şirul format din numerele: 1, 5, 7, 4, 6, 2, 9, secvenţa formată din numerele 7, 4, 6, 2 (corespunzătoare lui p=3 şi k=4) are gradul egal cu 2 deoarece, după ordonarea crescătoare a numerelor din secvenţă, aceasta devine 2, 4, 6, 7, numerele 4 şi 6 rămânând pe aceleaşi poziţii.
Scrieţi un program care citeşte numerele n, k, x1, x2, …, xn, cu semnificaţia din enunţ, şi apoi determină:
a) gradul întregului şir de numere;
b) poziţia primului element din prima secvenţă de lungime k ce are gradul maxim, precum şi gradul acestei secvenţe.
OJI 2011, Clasa a VI-a
- Fișiere
- Doru Popescu Anastasiu
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
#1065
Vase1
 Specialiştii chimişti au reuşit crearea în laborator a unei game diversificate de substanţe lichide nemiscibile (care nu se amestecă între ele), de aceeaşi densitate şi de culori diferite.
Specialiştii chimişti au reuşit crearea în laborator a unei game diversificate de substanţe lichide nemiscibile (care nu se amestecă între ele), de aceeaşi densitate şi de culori diferite.
Acest rezultat a fost utilizat de către specialiştii fizicieni pentru studiul principiului vaselor comunicante. Conform acestui principiu „într-un sistem de vase comunicante nivelul lichidului este acelaşi, indiferent de forma vaselor.“
Experimentele fizicienilor se desfăşoară astfel:
Într-un sistem cu două vase comunicante, gradat identic pe fiecare ramură cu 0, 1, 2, 3,…, fizicienii introduc un număr de n lichide, pe ramura din stânga sau pe ramura din dreapta. Volumele introduse din fiecare lichid, notate cu Vi (1≤i≤n), sunt numere naturale nenule pare astfel încât, la echilibru, orice lichid se va aşeza între două gradaţii de aceeaşi parte a unei ramuri sau pe cele două ramuri ale sistemului de vase comunicante. Lichidele sunt identificate prin intermediul culorii acestora, culori numerotate cu 1, 2, 3, … , n. Introducerea lichidelor în sistemul cu două vase comunicante se face în ordinea crescătoare a numerelor culorilor, începând cu lichidul de culoare 1.
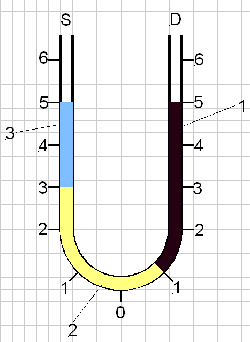 Scopul experimentului este de a determina gradaţia maximă la care se ridică lichidele în sistemul cu două vase comunicante, precum şi între ce gradaţii se găseşte un lichid de culoare
Scopul experimentului este de a determina gradaţia maximă la care se ridică lichidele în sistemul cu două vase comunicante, precum şi între ce gradaţii se găseşte un lichid de culoare x, dintre cele introduse.
De exemplu, dacă în sistemul cu două vase comunicante se introduc n=3 lichide în ordinea: V1=4 lichid de culoare 1 introdus prin ramura din dreapta (operaţie codificată 4 D), V2=4 lichid de culoare 2 introdus prin ramura din stânga (operaţie codificată 4 S) şi V3=2 lichid de culoare 3 introdus prin ramura din stânga (operaţie codificată 2 S) atunci gradaţia maximă la care se ridică nivelul lichidelor în sistemul cu două vase comunicante este 5, iar lichidul de culoare x=2 se găseşte între gradaţiile: 3 pe ramura din stânga (3 S) şi 1 pe ramura din dreapta (1 D), conform figurii alăturate.
Să se scrie un program care cunoscând numărul n de lichide introduse în sistemul cu două vase comunicante, volumul Vi şi ramura prin care se face introducerea lichidului de culoare i (1≤i≤n), precum şi culoarea x, să calculeze gradaţia maximă la care se ridică lichidele în acest sistem la echilibru şi între ce gradaţii se găseşte lichidul de culoare x.
OJI 2011, Clasa a IX-a
- Fișiere
- Ciprian Chesca
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse
#1066
AI
Institutul Naţional de Robotică Avansată realizează o serie de teste ultimei generaţii de roboţi inteligenţi proiectaţi de specialiştii acestuia. Sistemul de testare se bazează pe o reţea de senzori formată din n segmente egale dispuse orizontal şi n segmente egale dispuse vertical. Distanţa între două segmente alăturate orizontale, respectiv verticale este de 1 metru. Fiecare segment orizontal este în contact cu fiecare segment vertical. Denumim nod un punct în care un segment orizontal şi unul vertical vin în contact. Segmentele sunt numerotate: cele orizontale de sus în jos începând de la 1 iar cele verticale de la stânga la dreapta începând de la 1.
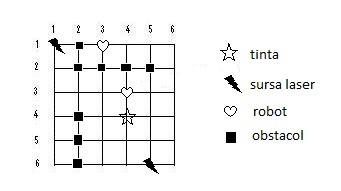 Un nod va fi identificat prin două numere: primul reprezintă numărul segmentului orizontal iar al doilea numărul segmentului vertical care vin în contact în respectivul nod.
Un nod va fi identificat prin două numere: primul reprezintă numărul segmentului orizontal iar al doilea numărul segmentului vertical care vin în contact în respectivul nod.
Într-unul dintre nodurile reţelei se află o ţintă. În alte două noduri se află câte o sursă ce emite o rază laser. O astfel de sursă emite raza într-o singură direcţie. Raza laser are o grosime neglijabilă. Cele două surse sunt astfel orientate încât raza emisă de fiecare “loveşte” ţinta. Cele două noduri în care sunt plasate sursele sunt astfel alese încât cele două raze nu se intersectează decât în nodul unde se află ţinta.
În alte două noduri ale reţelei se află câte un robot. Fiecare robot se poate deplasa dintr-un nod în cele vecine (cele aflate sus, jos, în stânga şi în dreapta), dar fără să iasă din cadrul reţelei. Roboţii se deplasează cu 1 m/secundă.
Se efectuează experimente în care roboţii sunt programaţi să se deplaseze prin reţea cu scopul de a proteja ţinta faţă de cele două raze laser. Un robot poate proteja ţinta fie ocupând nodul unde se află sursa, fie ocupând un nod prin care trece raza laser în drumul de la sursă către ţintă (razele laser nu “ocolesc” roboţii). Dimensiunea roboţilor este atât de mică încât, în acest al doilea caz, ei protejează ţinta faţă de raza laser doar când nodurile unde sunt sursa, ţinta şi robotul sunt coliniare iar robotul este între sursă şi ţintă. În momentul în care un robot ajunge într-un nod unde protejează ţinta faţă de una dintre raze, el se poate opri sau poate să îşi continue deplasarea. Dacă îşi continuă deplasarea astfel încât noua poziţie ocupată de acel robot şi poziţiile ţintei şi sursei nu mai sunt coliniare, atunci acel robot nu mai protejează ţinta. Din modul în care sunt alese poziţiile nodurilor pentru ţintă şi sursele laser rezultă că nu există nicio poziţie în care un robot să protejeze simultan ţinta faţă de ambele raze.
Fiecare robot este dotat cu o reţea neuronală şi poate învăţa din experimentele anterioare pe unde să se deplaseze. Pentru a mări capacitatea de adaptare a roboţilor, în k noduri ale reţelei sunt aşezate obstacole care fac ca roboţii să nu poată trece prin nodurile respective. Deoarece obstacolele folosite sunt transparente, razele laser pot trece prin acestea fără a le fi afectată intensitatea sau direcţia. Două sau mai multe obstacole dispuse pe acelaşi segment, în noduri alăturate, formează un zid. Lungimea unui zid este egală cu numărul de obstacole din care este alcătuit.
Cerințe:
1) Determinaţi lungimea maximă a unui zid.
2) Determinaţi numărul minim de secunde în care cei doi roboţi pot proteja ţinta faţă de cele două raze laser.
OJI 2011, Clasa a X-a
- Fișiere
- Stelian Ciurea, Daniela Marcu, Ovidiu Marcu
- concurs
- Clasa 10 Structuri de date liniare Coada
#1067
Expresie7
Prin convenţie numim expresie aritmetică ponderată o expresie construită astfel:
- expresia conţine numere întregi de cel mult
2cifre despărţite prin virgulă; - numim
k-șiro enumerare deknumere despărţite prin virgulă (k≥1); - o expresie poate conţine unul sau mai multe
k-şiruri; - expresia foloseşte paranteze rotunde şi paranteze drepte.
Fiind dată o expresie aritmetică ponderată să se determine:
- câte numere întregi conţine expresia aritmetică;
- care este valoarea expresiei aritmetice.
OJI 2011, Clasa a X-a
- Fișiere
- Eugen Nodea
- concurs
- Clasa 10 Probleme diverse Diverse
#1077
Litere
Algorel a primit un joc care conţine n jetoane pe care sunt scrise litere mari ale alfabetului. Fiecare literă are asociat un cod format dintr-o singură cifră nenulă. Jetoanele se aşează în ordinea dată iniţial, iar prin citirea literelor de pe acestea, de la primul la ultimul jeton, se formează un cuvânt. Dacă se citesc numerele de pe fiecare jeton, începând de la primul la ultimul, se obţine un număr k1. Jocul continuă la fel, dar se aşează jetoanele începând de la al doilea la ultimul, obţinându-se un nou număr k2. Apoi, se aşează jetoanele începând de la al treilea la ultimul, obţinându-se un nou număr k3, ş.a.m.d. până se ajunge la aşezarea doar a ultimului jeton, caz în care se obţine numărul kn.
Scrieţi un program care citeşte numărul n de jetoane, cele n litere asociate jetoanelor, precum şi codurile asociate literelor, în ordinea apariţiei lor şi afişează:
a) numărul de perechi de litere consecutive din cuvântul iniţial care au proprietatea că o literă este vocală şi cealaltă este consoană (ordinea lor nu contează);
b) numărul k1, format din aşezarea iniţială a jetoanelor;
c) suma k1+k2+…+kn.
OJI 2011, Clasa a VII-a
- Fișiere
- Adrian Pintea
- concurs
- Clasa 10 Şiruri de caractere Probleme diverse
- Siruri de caractere
- Numere mari