Lista de probleme 248

Ali Baba și cei 40 de hoți stăpânesc un deșert de formă dreptunghiulară, împărțit în n linii și m coloane, care definesc n*m sectoare. Intrarea într-un sector se plătește cu o taxă cunoscută, exprimată în galbeni.

Un călător trebuie să traverseze deșertul de la Est la Vest, trecând dintr-un sector în altul, astfel: din sectorul (i j) se poate ajunge în unul din sectoarele (i-1,j-1), (i,j-1) sau (i+1,j-1), dar fără a părăsi deșertul (ar fi omorât de oamenii lui Ali Baba). La trecerea printr-un sector, călătorul plătește taxa aferentă acelui sector.

Determinați suma totală minimă pe care trebuie să o plătească călătorul la traversarea deșertului, știind că pleacă din orice sector al coloanei m (Est) și se oprește în orice sector al coloanei 1 (Vest), cu respectarea condițiilor de mai sus.

Ali Baba și cei 40 de hoți stăpânesc un deșert de formă dreptunghiulară, împărțit în n linii și m coloane, care definesc n*m sectoare. Intrarea într-un sector se plătește cu o taxă cunoscută, exprimată în galbeni.

Un călător trebuie să traverseze deșertul de la Nord la Sud, trecând dintr-un sector în altul, astfel: din sectorul (i j) se poate ajunge în unul din sectoarele (i+1,j-1), (i+1,j) sau (i+1,j+1), dar fără a părăsi deșertul (ar fi omorât de oamenii lui Ali Baba). La trecerea printr-un sector, călătorul plătește taxa aferentă acelui sector.

Determinați suma totală minimă pe care trebuie să o plătească călătorul la traversarea deșertului, știind că pleacă din orice sector al liniei 1 (Nord) și se oprește în orice sector al liniei n (Sud), cu respectarea condițiilor de mai sus.

Se citește de la tastatură număr natural n. Pornind de la valoarea 1, asupra valorii curente x se pot aplica următoarele trei operații: înmulțire cu 2, înmulțire cu 3 sau adunare cu 1. De exemplu, dacă x=1 atunci se poate obține 2 (prin înmulțirea cu 2 sau prin adunarea cu 1) sau 3 (prin înmulțirea cu 3).

Calculați numărul minim de operații necesare pentru a obține numărul n începând de la numărul 1.

O tablă de șah se reprezintă ca o matrice cu n linii și n coloane în care pozițiile libere au valoarea 0, iar pozițiile ocupate de piese sunt marcate prin valoarea 1.

Să se determine numărul maxim de piese pe care le poate lua un pion care pleacă de pe prima linie a tablei și vrea să ajungă pe ultima linie. Pionul poate porni din orice poziție de pe prima linie. Pe prima linie nu se află alte piese.

Pionul aflat în pozitia i,j se poate deplasa astfel:

• în poziția i+1, j dacă este liberă
• în poziția i+1, j-1 dacă este o piesă în această poziție
• în poziția i+1, j+1 dacă este o piesă în această poziție

Pentru un număr natural nenul n, să se determine numărul de submulțimi ale mulțimii {1, 2,..., n} cu proprietatea că oricare două elemente dintr-o submulțime au diferența în modul strict mai mare decât 1.

În arhipelagul X, ajunge un peşte de aur. După drumul obositor parcurs de peşte, el vrea să se relaxeze într-o anumită zonă din acest arhipelag (cu coordonatele x2, y2). Totodată, acest peşte este curios să afle câte modalităţi sunt ca să ajungă în acea zonă.

În parcul orașului există 4 rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C și D, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:

O veveriță jucăușă sare prin copaci astfel:

• pornește dintr-un copac numerotat cu 1;
• la fiecare pas sare dintr-un copac numerotat cu i într-un copac numerotat cu i+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul D, va sări în copacul de pe rândul C, dacă se află în copacul de pe rândul B, va sări în copacul de pe rândul A sau în copacul de pe rândul C, iar dacă se află în copacul de pe rândul C, va sări în copacul de pe rândul B sau în copacul de pe rândul D;
• se oprește într-unul dintre copacii numerotați cu n.

Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.

Fie un vector cu n elemente numere naturale. Determinați suma maximă care se poate obține prin adunarea valorilor care nu se află pe poziții consecutive în vector.

În parcul orașului există 5 rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C, D și E, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:

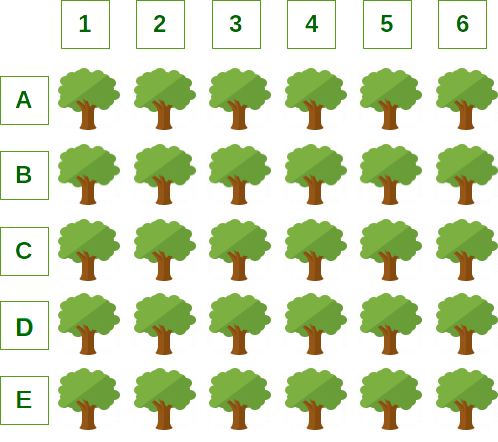
O veveriță jucăușă sare prin copaci astfel:

• pornește dintr-un copac numerotat cu 1;
• la fiecare pas sare dintr-un copac numerotat cu i într-un copac numerotat cu i+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul E, va sări în copacul de pe rândul D, dacă se află în copacul de pe rândul B, va sări în copacul de pe rândul A sau în copacul de pe rândul C, dacă se află în copacul de pe rândul C, va sări în copacul de pe rândul B sau în copacul de pe rândul D,iar dacă se află în copacul de pe rândul D, va sări în copacul de pe rândul C sau în copacul de pe rândul E;
• se oprește într-unul dintre copacii numerotați cu n.

Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.

Un numar natural se numeste “numar scara” daca toate cifrele lui sunt ordonate crescator, de la stanga la dreapta. De exemplu 11223569 este un “numar scara”, dar 98873 si 122429 nu sunt. Mihnea primeste o radiera si o foaie pe care este scris un sir de cifre. El trebuie sa stearga cat mai putine cifre cu proprietatea ca daca lipim cifrele ramase in ordinea din sir vom avea un “numar scara”.

Să se determine numărul minim de ștergeri pe care trebuie să le facă Mihnea.