Lista de probleme 41

Într-un depozit au fost așezate cutii identice, una după alta, eventual suprapuse, astfel încât numărul maxim de cutii suprapuse într-o stivă este N, iar între două stive cu același număr de cutii să existe cel puțin una cu mai multe cutii decât oricare dintre cele două. Considerăm că o stivă poate fi formată dintr-o singură cutie.

Să se determine numărul de submulțimi nevide ale mulțimii {1, 2,..., n} cu proprietatea că oricare două elemente dintr-o submulțime au diferența în modul strict mai mare decât 1.

În câte moduri se poate obține suma n aruncând cu zarul (În câte moduri poți să îl scrii pe n ca sumă de valori mai mici sau egale cu 6).

Să se afle câte numere naturale cu n cifre au suma oricăror două cifre alăturate pătrat perfect.

Se dă o tablă de șah cu n+1 linii (numerotate de sus în jos începând cu 1) și 2n+1 coloane (numerotate de la stânga la dreapta începând cu 1). Pe prima linie pătratul din mijloc conține 1 gram de fân, iar celelalte pătrate de pe prima linie nu conțin nimic. Începând cu linia a doua fiecare pătrat conține o cantitate de fân obținută prin adunarea cantităților de fân din cele 3 pătrate ale liniei anterioare cu care se învecinează (pe verticală și diagonală). De exemplu dacă n=3 tabla are 4 linii, 7 coloane și următoarea configurație.

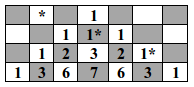
Un cal pleacă de pe prima linie, de pe o coloana k<=n, sare din orice poziție (i,j) în poziția (i+1,j+2) atât timp cât este posibil și mănâncă tot fânul din pătratele prin care trece. De exemplu, pentru n=3 și k=2, pătratele prin care trece calul sunt marcate cu asterisc ( * )

Cerinţe:

1. Cunoscând n și k, să se calculeze cantitatea de fân de pe linia k a tablei.
2. Cunoscând n și k, să se calculeze câte grame de fân mănâncă un cal care pleacă de pe prima linie, de pe coloana k.

Claudia vrea să construiască o scară cu N trepte astfel încât prima treaptă să fie la înălţimea 0 şi ultima treaptă să fie la înălţimea H. Fiind pusă pe glume, ea îi cere arhitectului să proiecteze o scară neobişnuită, în care treptele sunt dispuse astfel încât, la un moment dat, să poţi urca, coborî sau rămâne la acelaşi nivel. Pentru a fi uşor de urcat sau coborât, valoarea absolută a diferenţei dintre înălţimile la care se află oricare două trepte consecutive trebuie să fie mai mică sau egală cu o valoare dată, K. Nicio treaptă nu se poate afla la o înălţime negativă sau la o înălţime mai mare decât H.

Scrieţi un program care să determine numărul de scări diferite cu N trepte, ce pot fi construite respectând cerinţele Claudiei. Deoarece numărul de scări poate fi foarte mare, determinaţi restul împărţirii acestui număr la 666013.

Toată lumea cunoaște modelul de deblocare a telefoanelor sub formă de o matrice cu 3 linii și 3 coloane. Se pot trasa diferite modele de deblocare având un număr N de puncte prin care trecem, din fiecare punct putând merge la oricare vecin al lui. (Sunt maximum 8 vecini de exemplu pentru punctul din mijloc și 3 vecini pentru un punct din colț).

Determinați câte variante de modele sunt posibile trecând prin N puncte. Deoarece numărul poate fi foarte mare, se va afișa numărul de variante modulo 1000003.

Avem un coridor lung de lățime k și lungime n. Avem sarcina de a-l acoperi cu bucăți de gresii de dimensiuni 1 x k, 2 x k și 3 x k. Calculați în câte moduri distincte se poate acoperi coridorul cu cele 3 tipuri de gresii. Pentru că rezultatul este un număr mare, se cere restul împărțirii la 1.000.000.007.

Aleku Turcul este la ora de matematica. În timp ce el încearcă să-și dea seama dacă 1+1=2, profesorul scrie pe tablă o problemă ceva mai complicată. Se dau Q queryuri și o listă S cu P elemente egale cu 0. Notăm cu A un șir, care inițial este vid. Queryurile pot fi de forma:
- 0 x (inserează valoarea x în A)
- 1 x (șterge valoarea x din A; se garantează că există cel puțin o valoare de x în A)
Se garantează că A nu va fi niciodată vid după vreun query. După fiecare query profesorul îi pune lui Aleku următoarea întrebare: oare pot așeza în lista S toate numerele din A (nu neapărat în ordinea în care se află în A) astfel încât:

• elementele din A se vor așeza în S pe poziții distincte, restul pozițiilor din S fiind ocupate de elemente cu valoarea 0
• fie S[i] un element nenul din S și S[j] cel mai apropiat element nenul care se află în stânga lui S[i] în S. Atunci următoarea condiție trebuie respectată: i - j ≥ S[i]
• fie f poziția celui mai din stânga element nenul din S. Atunci f ≥ S[f].

Dacă răspunsul la întrebarea profesorului este da, atunci să se spună și câte configurații diferite se pot obține. Deoarece răspunsul la întrebare poate fi foarte mare, acesta se va afișa modulo 1.000.000.007. Dacă răspunsul este nu, se va afișa -1.
Ajutați-l pe Aleku sa răspundă corect la întrebările profesorului pentru ca sa obțină nota 10. Media lui depinde de aceasta!

Se dau două numere N și M urmate de un șir de numere întregi nenule S de lungime impară N indexat de la 0. Asupra acestuia se vor efectua fix M operații de swap. O operație reprezintă selectarea la întâmplare a doi indici (nu neapărat distincți) din intervalul [0, N – 1] și interschimbarea elementelor de pe pozițiile respective. Se consideră că șirul este alternant dacă nu există elemente alăturate având același semn. Determinați probabilitatea ca la finalul celei de-a M-a operații, șirul să fie alternant. (Se garantează că există cel puțin o aranjare a șirului astfel încât acesta să fie alternant). Se poate demonstra că probabilitatea cerută se poate reprezenta sub forma P / Q unde P si Q sunt prime între ele.