Lista de probleme 41

Se dă n un număr natural. Într-un şir de lungime n, format cu cifrele 0 şi 1, numim insulă o secvenţă maximă de cifre egale. Să se afle câte insule se află în toate şirurile de lungime n, formate cu cifrele 0 şi 1.

Astăzi în clasa 0 profesoara a numit Q copii și le-a dat 3 numere, a, b și c, copiii trebuiau să spună care este rezultatul calculului $a^{C_b^c}$, adică $a^{\frac{b!}{c!\ast (b-c)!}}$, modulo ${10}^9+7$. Copiii nu au știut să răspundă la întrebări așa că voi trebuie acuma să le spuneți rezultatul.

Spionul 008 vrea să găsească o locație secretă în junglă, având asupra lui un dispozitiv de localizare. Iniţial spionul se află la intrarea în junglă pe nivelul 1 şi cu fiecare pas, el avansează de la nivelul i la nivelul i+1, ajungând la locaţia secretă, aflată pe ultimul nivel, în poziţia u faţă de marginea stângă a nivelului curent. Pentru a ajunge în locaţia secretă, el poate să se deplaseze cu o poziţie spre Sud-Est (codificat cu caracterul E) sau spre Sud-Vest (codificat cu caracterul V), trecând de pe nivelul i pe nivelul i+1 cu viteză constantă. Numărul de poziţii de pe un nivel creşte cu unu faţă de nivelul anterior, conform imaginii alăturate. Numim traseu o succesiune formată din caracterele E sau V, corespunzătoare deplasării spionului de pe nivelul 1 la locaţia secretă. Pentru exemplul din figura alăturată succesiunea de caractere VEEVE reprezintă un traseu ce corespunde locaţiei secrete din poziţia 4 a nivelului 6.

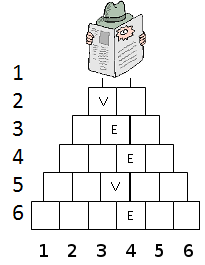
Cunoscând succesiunea de caractere corespunzătoare unui traseu, determinaţi:
a) poziţia locației secrete de pe ultimul nivel;
b) numărul de trasee distincte pe care le poate urma spionul plecând din poziţia inițială pentru a ajunge în locaţia secretă corespunzătoare traseului dat. Două trasee se consideră distincte dacă diferă prin cel puţin o poziţie.

Fie N un număr natural cu proprietatea că (N, 10) = 1.
Să se determine lungimea perioada T a fracţiei zecimale periodice simple $\frac{1}{N}$

În Hogwarts există o tablă de șah cu N linii și M coloane. Harry Potter a găsit plasate, de către Hagrid, T ture care apără fiecare linia și coloana pe care este așezată. El trebuie să plaseze în siguranță K pioni pe tablă, adică fără ca vreunul dintre ei să fie atacat de vreo tură. Tabla de șah din Hogwarts este specială deoarece în cadrul unei celule pot fi plasați chiar și mai mulți pioni simultan! Cunoscând toate aceste reguli, ajutați-l pe Harry Potter să determine în câte modalități poate plasa în siguranță toți cei K pioni pe tabla de șah.

In plină perioadă de pandemie, cercetătorii unui institut vor să facă o serie de experimente pe culturi de celule. S-a observat deja că celula cercetată are o creștere liniară dependentă de cele trei zile imediat anterioare: dacă acum două zile aveam x celule, ieri aveam y iar astăzi avem z celule, atunci mâine vom avea x+ay+bz celule. Dacă într-o zi, numărul de celule depășește o valoare k, cercetătorii reduc cultura la valoarea modulo K.

Dacă, pentru un n dat, se cunoaște numărul de celule din zilele n, n-1, n-2 și se cunosc factorii de multiplicare a și b, care este numărul de celule care trebuie cultivate în primele 3 zile ale experimentului?

Un număr este special dacă are o cifră cu frecvența strict mai mare decât partea întreagă a jumătății lungimii numărului și nu conține cifra 0. Câte numere speciale există respectiv care este suma tuturor numerelor speciale de lungime N.

Se dă N și Q, apoi Q interogări de tipul K X pentru fiecare interogare să se afișeze separate prin spațiu ( ficare interogare pe un rând diferit ):

1. Câți vectori de exact N elemente din intervalul $[0,2^K)$ ( mai mari sau egale cu $0$ și strict mai mici ca $2^K$ ) există astfel încât valoarea $a_1$ & $a_2$ & ... & $a_N$ să fie X-frumoasă. Un număr este X-frumos dacă în reprezentare binară are exat X biți setați ( cu valoare = 1 ). Cu & am notat operația pe biți AND.

2. Câți vectori de exact N elemente din intervalul $[0,2^K)$ ( mai mari sau egale cu $0$ și strict mai mici ca $2^K$ ) există astfel încât valoarea $a_1$ | $a_2$ | ... | $a_N$ să fie X-frumoasă. Un număr este X-frumos dacă în reprezentare binară are exat X biți setați ( cu valoare = 1 ). Cu | am notat operația pe biți OR.

3.Câți vectori de exact N elemente din intervalul $[0,2^K)$ ( mai mari sau egale cu $0$ și strict mai mici ca $2^K$ ) există astfel încât valoarea $a_1$ ^ $a_2$ ^ ... ^ $a_N$ să fie X-frumoasă. Un număr este X-frumos dacă în reprezentare binară are exat X biți setați ( cu valoare = 1 ). Cu ^ am notat operația pe biți XOR.

Aveți la dispoziție toate numerele naturale de la 1...M pentru a forma vectori de lungime N. De exemplu , Pentru N = 3 și M = 200 , un posibil vector este [199 , 41 , 41]. Pentru fiecare vector distinct care poate fi creat ( doi vectori A și B sunt distincți dacă există cel puțin un i astfel încât A[i] != B[i]) , se cere să determinați cel mai mare divizor comun al elementelor sale. Care este suma valorilor determinate ?

RAU-Gigel își serbează ziua alături de colegii săi de la clubul de informatică și vrea să le împartă bomboane. El are un număr dat de bomboane și ar vrea să știe dacă îi ajung și, dacă da, în câte moduri le poate împărți. Dar nu își amintește câți colegi are la cerc, are însă o informație care ar putea să îl ajute.