Lista de probleme 41

Filtrare

Mai multe opțiuni

Fibonacci2

#3344

Șirul lui Fibonacci este definit astfel:

$F_{n} = {\begin{cases} 1 & dacă n = 1 sau n = 2, \\ F_{n - 1} + F_{n - 2} & dacă n > 2. \end{cases}$

Se dă un număr natural n. Determinați al n-lea termen al șirului, modulo 666013.

Consola Silviu Candale medie Clasa 11 Probleme diverse Matematica Exponentiere rapida

Rezolvă

Numim suma cifrelor până la o cifră a unui număr X, o valoare mai mică decât 10 obținută prin adunarea cifrelor numărului X și repetarea procedurii dacă suma obținută este mai mare decât 10, de această dată având drept X suma obținută la pasul precedent.

Se dau două numere a și b. Calculați suma cifrelor pana la o cifra a lui $a^{b}$ .

Consola Măierean Mircea dificilă Clasa 11 Probleme diverse Matematica Exponentiere rapida

Rezolvă

summy

#3123

Se dau n şi k numere naturale. Calculați suma $\sum_{i = 1}^{n} i^{k}$ .

***

Consola Mihai Bunget dificilă Clasa 11 Probleme diverse Matematica Exponentiere rapida Invers modular

Rezolvă

rogvaiv

#2018

Vecinul meu, Dorel, tocmai s-a mutat la casă şi vrea să-şi vopsească gardul. Fiind îndrăgostit de frumos, a cumpărat 7 cutii de vopsea: roşu, orange, galben, verde, albastru, indigo şi violet. Acum însă, are o dilemă: în câte moduri poate vopsi cele n uluci ale gardului, ştiind că fiecare ulucă poate fi vopsită cu oricare dintre culorile cumpărate?

mathland

Fișiere Mihai Bunget dificilă Clasa 11 Probleme diverse Probleme diverse Numere mari Exponentiere rapida

Rezolvă

fibona

#2773

Dorel tocmai a aflat despre existenţa şirului lui Fibonacci: F₀=0, F₁=1, F₂=1, F₃=2, F₄=3, F₅=5,… . Pentru numerele n, k şi p date, Dorel vă roagă să calculaţi suma F_p + F_k+p + F_2•k+p + … + F_n•k+p.

nEUROn

Consola Mihai Bunget dificilă Clasa 11 Probleme diverse Matematica Fibonacci Exponentiere rapida

Rezolvă

dinamica06

#3990

Se dă un număr natural nenul n. Să se determine numărul de numere de n cifre din mulțimea {1, 2, 3, 4} care nu au două cifre alăturate egale și care au proprietatea că sunt divizibile cu 2. Pentru că acest număr poate fi foarte mare, se va calcula modulo 123457.

Folclorul informatic

Consola Dan Pracsiu ușoară Clasa 11 Programare dinamică Probleme de numărare Exponentiere rapida

Rezolvă

dinamica07

#4504

Se dau numerele naturale n, p și q. Să se determine numărul șirurilor de n biți în care numărul biților de 1 este cuprins între p și q.

Folclorul informatic

Consola Dan Pracsiu medie Clasa 11 Programare dinamică Probleme de numărare Combinari Invers modular Exponentiere rapida

Rezolvă

Veverita4

#4287

În parcul orașului există 4 rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C și D, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:

O veveriță jucăușă sare prin copaci astfel:

pornește dintr-un copac numerotat cu 1;
la fiecare pas sare dintr-un copac numerotat cu i într-un copac numerotat cu i+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul D, va sări în copacul de pe rândul C, dacă se află în copacul de pe rândul B, va sări în copacul de pe rândul A sau în copacul de pe rândul C, iar dacă se află în copacul de pe rândul C, va sări în copacul de pe rândul B sau în copacul de pe rândul D;
se oprește într-unul dintre copacii numerotați cu n.

Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.

Fișiere medie Clasa 11 Programare dinamică Probleme de numărare Numere mari Exponentiere rapida

Rezolvă

VeveritaK

#4289

În parcul orașului există k rânduri de câte n copaci perfect aliniați. Rândurile sunt notate A, B, C … K, iar copacii de pe fiecare rând sunt numerotați de la 1 la n, ca în imaginea de mai jos:

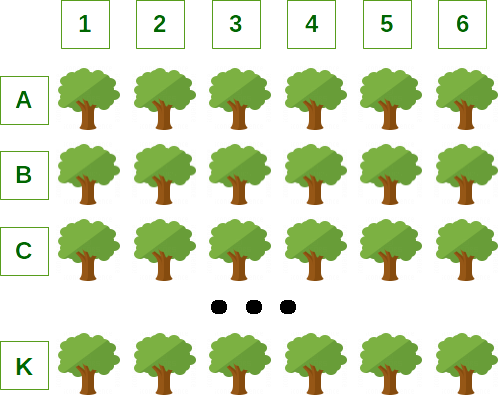
O veveriță jucăușă sare prin copaci astfel:

pornește dintr-un copac numerotat cu 1;
la fiecare pas sare dintr-un copac numerotat cu i într-un copac numerotat cu i+1. Dacă se află într-un copac de pe rândul A, va sări în copacul de pe rândul B, dacă se află într-un copac de pe rândul K, va sări în copacul de pe rândul K-1. Dacă se află în copacul de pe unul dintre rândurile B, C, D, …K-1 va sări în copacul de pe rândul anterior sau în copacul de pe rândul următor. De exemplu, dacă se află în copacul de pe rândul D, va sări în copacul de pe rândul C sau în copacul de pe rândul E;
se oprește într-unul dintre copacii numerotați cu n.

Aflați numărul M de modalități în care se poate deplasa veverița, respectând regulile de mai sus.

Fișiere medie Clasa 11 Programare dinamică Probleme de numărare Exponentiere rapida

Rezolvă

dinamica04

#3214

Definim un număr natural ca fiind bun dacă toate cifrele impare se află înaintea celor pare. De exemplu, numerele 13424, 400, 1357 sunt bune, pe când 34010 nu este. Dându-se un număr natural nenul n, să se determine câte numere bune de n cifre există.

Consola Dan Pracsiu ușoară Clasa 11 Programare dinamică Probleme de numărare Exponentiere rapida

Rezolvă

Du-te sus!