Lista de probleme 17
Nivelul concursului: Județean
http://olimpiada.info/oji2020/index.php
Grupe
Clasa a V-a Clasa a VI-a Clasa VII-a Clasa VIII-a Clasa a IX-a Clasa a X-a Clasele XI-XII
#3431
Cartonase3
Ionel are N cartonașe. Fiecare cartonaș are înscrise două numere (un număr, s, în partea stângă, și celălalt număr, d, în partea dreaptă). El a așezat cartonașele într-un șir, lipite unul de celălalt, astfel încât numărul din partea dreaptă a primului cartonaș este lipit de numărul din partea stângă a celui de-al doilea cartonaș, numărul din partea dreaptă a celui de al doilea cartonaș este lipit de numărul din partea stângă a celui de-al treilea cartonaș etc. Spunem că două cartonașe alăturate “se potrivesc” dacă numărul din dreapta al primului cartonaș este egal cu numărul din stânga al celui de al doilea cartonaș. Scrieți un program care să citească numărul N de cartonașe, numerele înscrise pe fiecare cartonaș și determină:
1) Numărul de perechi de cartonașe care “se potrivesc”.
2) Numărul de cartonașe din cea mai lungă secvență în care fiecare două cartonașe alăturate “se potrivesc”.
3) Numărul de secvențe cu număr maxim de cartonașe care “se potrivesc”.
OJI 2020, clasa a V-a
- Fișiere
- Adriana Simulescu
- concurs
- Clasa 9 Algoritmi elementari Probleme diverse
#3440
Buldo
Dorești să nivelezi terenul pe care l-ai cumpărat, care are lățimea de 1 metru și lungimea de N metri, fiind alcătuit din N zone succesive, fiecare zonă având lungimea de 1 metru. Terenul se reprezintă ca un șir de N numere naturale h1, h2, h3, …, hN reprezentând înălțimile în metri pe care le au zonele din terenul inițial, privite de la stânga spre dreapta.
Pentru a nivela terenul ai închiriat un buldozer care funcționează astfel. Se alege o înălțime H (număr natural) la care ridicăm lama buldozerului. Inițial buldozerul are pe lamă o cantitate C=0 metri cubi de pământ. Buldozerul începe să mergă de la stânga la dreapta și când ajunge la zona i, în funcție de înălțimea hi a acesteia, se va afla în una dintre următoarele situații:
- dacă
hi≥ Hatunci cantitatea suplimentarăhi- Hse adaugă laCși nivelul zonei ajunge laH. - dacă
hi< Hatunci se scade dinCdiferențaH - hipentru a aduce nivelul zonei la nivelulH.
Remarcăm faptul că H trebuie ales inițial astfel încât de fiecare dată când buldozerul ajunge în a doua situație să aibă pe lamă suficient pământ (C ≥ H - hi). După ce buldozerul parcurge cele N zone de lungime 1 pe lama buldozerului e posibil să mai rămână pământ, dar asta nu te interesează, pentru că la capătul din dreapta al terenului este un râu, și pământul rămas se va vărsa acolo.
Scrieţi un program care calculează înălțimea maximă H la care poate fi ridicată lama, astfel încât terenul să poată fi nivelat la acea înălțime.
OJI 2020, clasa a IX-a
- Fișiere
- Marius Nicoli
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Căutare binară
#3436
Wind
Domnul Vânt a pus pe marginea unei șosele N centrale eoliene, dintre care unele produc energie electrică, iar altele, deocamdată, doar consumă energie. El a etichetat centralele cu numerele naturale distincte de la 1 la N, în ordinea poziționării lor pe șosea. Fiecare centrală eoliană are la bază un ecran pe care este afișat un număr întreg, reprezentând cantitatea de energie pe care o produce (dacă numărul este pozitiv) sau pe care o consumă (dacă numărul este negativ).
Pentru a construi corect k orașe de-a lungul acestei șosele, un arhitect trebuie să aibă în vedere că:
- fiecărui oraș îi va fi atribuit câte un grup format din centrale eoliene vecine pe șosea, toate grupurile având același număr de centrale;
- cantitatea de energie repartizată unui oraș este egală cu suma numerelor afișate pe ecranele centralelor
eoliene din grupul atribuit; uneori este posibil ca, deocamdată, suma obținută să fie negativă; - fiecare dintre cele
Ncentrale eoliene trebuie să fie atribuită unui oraș; - factorul de dezechilibru, notat cu
P(k), este valoarea maximă a diferenței dintre energiile repartizate oricăror două orașe diferite, dintre celek.
Scrieți un program care citește numărul N, valorile afișate pe cele N ecrane ale centralelor eoliene și rezolvă următoarele două cerinţe:
- afișează numărul
Mde moduri în care se pot grupa celeNcentrale pentru construcția corectă de orașe; - afișează numărul maxim
Xde orașe ce pot fi construite corect, dintre cele care au factorul de dezechilibru minim, precum și etichetaEa primei centrale eoliene atribuită orașului cu cea mai mare cantitate de energie repartizată, dintre celeXorașe; dacă sunt mai multe astfel de orașe, se ia în considerare cel care are atribuite centrale etichetate cu numere mai mari.
OJI 2020, clasa a VII-a
- Fișiere
- Flavius Boian
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme cu secvențe
#3433
Forta
Forța unui număr natural nenul X este egală cu numărul de divizori pozitivi ai lui X. De exemplu, numărul X = 10 are forţa 4, deoarece 10 are 4 divizori, mulțimea divizorilor fiind D10 = {1,2,5,10}.
Scrieţi un program care, cunoscând un șir de n numere naturale nenule, rezolvă următoarele cerințe:
1. determină cel mai mic număr din șir care are forța maximă;
2. determină lungimea maximă a unei secvențe formată din numere cu aceeași forţă ce poate fi obținută prin rearanjarea convenabilă a elementelor din șir.
OJI 2020, clasa a VI-a
- Fișiere
- Raluca Costineanu
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme cu secvențe
- Descompunere in factori
- ciurul lui Eratostene
#3438
Triunghi5
Se consideră A un tablou bidimensional cu n linii, n coloane și elemente numere naturale. O zonă triunghiulară a tabloului, reprezentată de tripletul (lin, col, k), este o zonă de forma unui triunghi dreptunghic cu catetele de lungime egală cu |k|, definită astfel:
- Pentru
k>0, zona este compusă dinklinii:- pe prima linie a zonei se află elementele
A[lin][col],A[lin][col+1], …,A[lin][col+k-1]; - pe a doua linie a zonei se află elementele
A[lin+1][col],A[lin+1][col+1], …,A[lin+1][col+k-2]; - pe a treia linie a zonei se află elementele
A[lin+2][col],A[lin+2][col+1], …,A[lin+2][col+k-3]; - …
- pe ultima linie a zonei se află elementul
A[lin+k-1][col].
- pe prima linie a zonei se află elementele
- Pentru
k<0, zona este compusă din|k|=-klinii:- pe prima linie a zonei se află elementul
A[lin-|k|+1][col]; - pe a doua linie a zonei se află elementele
A[lin-|k|+2][col-1],A[lin-|k|+2][col]; - …
- pe ultima linie a zonei se află elementele
A[lin][col-|k|+1],A[lin][col-|k|+2],…,A[lin][col].
- pe prima linie a zonei se află elementul
Suma elementelor ce compun o zonă triunghiulară se numește suma zonei.
Scrieţi un program care, cunoscând tabloul A şi Q zone triunghiulare, determină cea mai mare dintre sumele zonelor.
OJI 2020, clasa a VIII-a
- Fișiere
- Alin Burța
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Parcurgerea matricelor oarecare
- Sume parțiale
#3435
foto1
O fotografie alb-negru a surprins imaginea fulgerelor pe cerul întunecat în timpul unei furtuni electrice. Mărită, fotografia arată ca un caroiaj format din mici pătrate identice, albe sau negre, dispuse alăturat pe N rânduri și M coloane, câte M pe fiecare rând. Pătratele albe formează fulgerele din fotografie, iar pătratele negre reprezintă cerul. În fotografie, nu există două pătrate albe dispuse alăturat pe același rând. Un fulger este format din pătrate albe situate pe rânduri consecutive care respectă următoarele condiții: a) pătratele albe situate pe două rânduri consecutive au un vârf comun sau o latură comună; b) un fulger poate avea un singur pătrat alb pe un rând. În fotografie, fulgerele sunt distincte, ele neavând pătrate albe cu laturi sau vârfuri comune. Înălțimea unui fulger este dată de numărul de pătrate albe ale acelui fulger.
Scrieți un program care citește numerele N și M, cele N*M elemente ale tabloului T care codifică fotografia și rezolvă următoarele cerințe:
- afișează numărul maxim
Pde pătrate negre dispuse alăturat pe un rând în fotografie; - afișează numărul
Fde fulgere și înălțimea maximăHa unui fulger din fotografie.
OJI 2020, clasa a VII-a
- Fișiere
- Carmen Minca
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Parcurgerea matricelor oarecare
#3442
SpiralMatrix
Parcurgând elementele unei matrice pătratice de dimensiune n în spirală, pornind din colțul din
stânga-sus, în sens orar, de la margini către interior, se obține șirul strict crescător format din toate
valorile de la 1 la n2, ca în figura de mai jos. Din șirul dat se obțin două subșiruri disjuncte, de lungime egală, cu număr maxim de termeni. Primul subșir este format din numere consecutive din prima jumătate a șirului, și trebuie să conțină în mod obligatoriu valoarea 1, iar al doilea este format din numere consecutive din a doua jumătate a șirului și trebuie să conțină în mod obligatoriu valoarea n2.
| 1 | 2 | 3 | 4 | 5 |
| 16 | 17 | 18 | 19 | 6 |
| 15 | 24 | 25 | 20 | 7 |
| 14 | 23 | 22 | 21 | 8 |
| 13 | 12 | 11 | 10 | 9 |
Să se afle poziția în matrice a celui mai mare termen din primul subșir și a celui mai mic termen din al
doilea subșir.
OJI 2020, clasa a IX-a
- Fișiere
- Marcel Dragan
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
- Cautare binara
#3441
Cetate
Cetatea Vizima din regatul Temeria poate fi reprezentată printr-o matrice cu N linii și M coloane, numerotate începând cu 1. Vizima este o cetate înfloritoare, fapt datorat numărului mare de negustori și meșteri prezenți. Din acest motiv, fiecărei celule din matrice îi este atribuit un profit corespunzător zonei respective. Regele Foltest dorește să reconstruiască zidurile cetății, dar cum războiul cu Imperiul Nilfgaard bate la ușă și resursele regatului sunt limitate, el trebuie să aleagă o porțiune pe care să o poată apăra, reprezentată ca o submatrice. O submatrice este identificată printr-o configurație de patru numere i1, j1, i2, j2 (1≤i1≤i2≤N, 1≤j1≤j2≤M), în această ordine, și este formată din elementele situate pe liniile consecutive i1, i1+1, …, i2 și pe coloanele consecutive j1, j1+1, …, j2 ale matricei prin care este reprezentată cetatea. Laturile submatricei sunt egale cu numărul de linii, respectiv de coloane din care a preluat elemente, iar profitul submatricei este suma valorilor din celulele sale.
Scrieţi un program care, cunoscând matricea cetății și o valoare K, determină:
- profitul maxim al unei submatrice cu laturile egale cu
K, precum și configurația prin care se identifică ea; - profitul maxim al unei submatrice cu laturile cel mult egale cu
K, precum și configurația prin care se identifică ea.
OJI 2020, clasa a IX-a
- Fișiere
- Iordache Ioan-Bogdan
- concurs
- Clasa 9 Tablouri bidimensionale (matrice) Probleme diverse
- Sume parțiale
#3432
Tai
Un număr este prim dacă are exact doi divizori naturali. Prin tăierea unui număr în p părți înțelegem împărțirea acestuia în p numere, fiecare de cel puțin o cifră, astfel încât prin alipirea numerelor obținute de la stânga la dreapta obținem numărul inițial.
De exemplu, dacă împărțim numărul 12045 în două părți avem patru variante de tăiere obținându-se numerele: 1 și 2045; 12 și 045; 120 și 45; 1204 și 5. Dacă îl împărțim în trei părți avem șase variante de tăiere obținându-se numerele 1, 2 și 045; 1, 20 și 45; 1, 204 și 5; 12, 0 și 45; 12, 04 și 5; 120, 4 și 5.
Se consideră un șir format din N numere naturale.
1) Determinați cel mai mare număr prim din șirul celor N numere.
2) Determinați cel mai mare număr prim dintre cele obținute prin tăierea în două părți a fiecărui număr din șirul celor N.
3) Determinați cel mai mare număr prim dintre cele obținute prin tăierea în trei părți a fiecărui număr din șirul celor N.
OJI 2020, clasa a V-a
- Fișiere
- Octavian Dumitrascu
- concurs
- Clasa 9 Algoritmi elementari Cifrele unui număr
#3434
Furnica1
Cercetătorii au descoperit că activitatea miriapodelor este stimulată de culoarea galben și de aceea o furnică este supusă unui experiment. Pe marginea mesei pe care se realizează experimentul s-au lipit una lângă alta, N foi dreptunghiulare, de culoare galbenă, numerotate în ordine, de la stânga la dreapta, de la 1 la N. Furnica se află pe masă, în fața primei foi și urmează un traseu deplasându-se doar pe laturile libere ale foilor (care nu sunt lipite de alte foi sau de masă), pe verticală sau orizontală, (așa cum indică săgețile din imaginea de mai jos), ajungând din nou pe masă. Știind că în urcare furnica parcurge un centimetru în 5 secunde, în coborâre parcurge un centimetru în 2 secunde, iar dacă se deplasează pe orizontală parcurge un centimetru în 3 secunde, ajutați-i pe cercetători să obțină unele date.
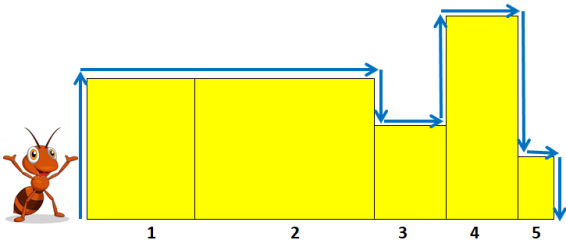
Scrieţi un program care să rezolve următoarele cerințe:
- determină timpul (exprimat în secunde) necesar furnicii pentru a parcurge tot traseul menționat;
- determină lungimea maximă (exprimată în centimetri) a unei porțiuni de traseu în care furnica NU coboară
deloc; - determină ce număr de ordine are foaia pe care se află furnica după
Tsecunde.
OJI 2020, clasa a VI-a
- Fișiere
- Cristina Iordaiche
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Probleme diverse