Lista de probleme 10
Nivelul concursului: Interjudețean
http://www.balcescucj.ro/moisil/
Grupe
Clasa a V-a Clasele VII-VIII Clasa a IX-a Clasa a X-a Clasele XI-XII
#627
Tripar
Mihai a găsit pe facebook o poză cu triunghiuri echilaterale aşezate în formă de piramidă, ca în figura de mai jos. El observă că piramida este compusă din mai multe benzi. Prima bandă conţine un triunghi echilateral, a doua bandă conţine 3 triunghiuri echilaterale, dintre care cel din mijloc este cu vârful în jos, a treia bandă conţine 5 triunghiuri echilaterale şi aşa mai departe.
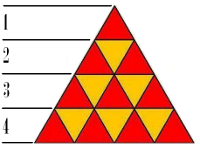
El constată că fiecare triunghi de cea mai mică dimensiune poate fi divizat în mai multe triunghiuri și mai mici prin procedeul de împărțire a unui triunghi. Prin acesta se înțelege unirea mijloacelor laturilor triunghiului, două câte două, printr-un segment, obținându-se astfel 4 triunghiuri mai mici ce compun triunghiul respectiv, ca în figura următoare.
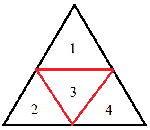
Mihai a analizat acest proces și a stabilit că dacă un triunghi este supus procedeului de împărțire, atunci toate triunghiurile din piramidă de dimensiunea lui vor trece prin acest procedeu. Astfel, el își pune următoarea întrebare: având N piramide, fiecare având un anumit număr de benzi, câte triunghiuri de cea mai mică dimensiune și câte perechi de drepte paralele are fiecare piramidă, după ce s-a executat procedeul de împărțire de M ori pe toate piramidele?
În prima figură o pereche de drepte paralele este formată din dreapta situată între benzile 2-3 și o dreaptă situată între benzile 3-4.
Cunoscând N, M și câte benzi are fiecare piramidă, se cere să se afișeze:
a) câte triunghiuri de cea mai mică dimensiune are fiecare piramidă, după executarea procedeului de împărțire de M ori;
b) câte perechi de drepte paralele are fiecare piramidă, după executarea procedeului de împărțire de M ori.
Grigore Moisil, 2014
- Fișiere
- concurs
- Clasa 9 Algoritmi elementari Sume, produse, numărări
#622
Multimi2
David a învățat de curând la școală ce înseamnă o mulțime de numere naturale și ce operații se pot face pe mulțimi. Printre operațiile învățate, lui David i s-au părut interesante operația de reuniune a două mulțimi și operația de intersecție a două mulțimi, așa că el, fiind pasionat de informatică, s-a gândit să implementeze cele două operații pentru două mulțimi. Mulțimile sunt formate din numere consecutive. Prima mulțime este formată din N numere naturale consecutive și începe cu P1, respectiv a doua mulțime este formată din M numere naturale și începe cu P2.
Cunoscând N, P1, M și P2 se cere:
a) Să se afișeze reuniunea celor două mulțimi.
b) Să se afișeze intersecția celor două mulțimi.
Grigore Moisil, 2014
- Fișiere
- Serban Alexandru Florian
- concurs
- Clasa 9 Elemente de baza ale limbajului Structuri repetitive
#624
Sah1
Alex dorește să își învețe fratele să joace șah. După ce i-a explicat regulile, Alex vrea să vadă dacă fratele lui a înțeles, aşa că îi dă un mic test. Având o tablă de șah de N linii şi N coloane, Alex pune pe ea M ture (tura atacă doar pe coloana și linia pe care se află) și un rege. Apoi îi cere fratelui său să îi spună de câte ture este atacat regele în acel moment și pe câte căsuțe de pe tablă poate fi pus regele, astfel încât să nu se afle în șah.
Cunoscând dimensiunea N a tablei de șah, poziția regelui de pe tablă, numărul M de ture și poziția fiecărei ture de pe tablă, se cere:
a)să se afișeze numărul de ture care atacă regele în acel moment;
b)numărul de poziții în care regele poate fi pus, astfel încât să nu fie atacat de vreo tură.
Grigore Moisil, 2014
- Fișiere
- Serban Alexandru Florian
- concurs
- Clasa 9 Tablouri unidimensionale (vectori) Vectori caracteristici / de frecventa
#623
Numere3
Având o pasiune pentru numere, Răzvan a inventat un nou joc pentru două persoane. Regulile jocului sunt simple: se aleg trei numere naturale a, b şi c astfel încât a<b<c. La fiecare pas, primul jucător adună la a suma cifrelor lui a, iar cel de-al doilea jucător scade din c suma cifrelor lui c, la pasul următor fiind luate în considerare noile valori obţinute pentru a şi c. Jocul se termină când, la un anumit pas, a devine mai mare sau egal decât b, caz în care primul jucător este declarat câştigător, sau când c devine mai mic sau egal cu b, situaţie în care câştigă al doilea jucător. Dacă la un pas se îndeplinesc ambele codiţii, jocul se termină la egalitate.
Cunoscând a, b şi c se cere:
a) Suma cifrelor celor trei numere.
b) Valorile numerelor a şi c la fiecare pas al jocului, precum şi câştigătorul jocului.
Grigore Moisil, 2014
- Fișiere
- Nicolae Dragos
- concurs
- Clasa 9 Algoritmi elementari Cifrele unui număr
#628
Cub1
Lui Andrei îi plac foarte mult jocurile de tip puzzle. De curând, el a descoperit un joc nou: un cub de dimensiune n format din n•n•n cuburi unitate sub forma unor cămăruţe. Cubul poate fi văzut ca o matrice tridimensionala ale cărei elemente sunt cămăruţele. Două cămăruţe se numesc adiacente dacă au o faţă comună. Astfel, o cămăruţă poate fi adiacentă cu maxim 6 cămăruţe. Scopul jocului este acela de a duce o bilă din cămăruţa de coordonate (1,1,1) în cămăruţa de coordonate (n,n,n). Bila poate trece dintr-o cămăruţă în alta doar dacă acestea sunt adiacente, iar noua cămăruţă este accesibilă din cămăruţa curentă.
Cunoscând n, dimensiunea cubului şi valorile asociate fiecărei cămăruţe, determinaţi:
a) cămăruța cu un număr maxim de cămăruțe ce pot fi accesate din ea;
b) un drum de lungime minimă de la cămăruţa (1,1,1) la cămăruţa (n,n,n).
Grigore Moisil, 2014
- Fișiere
- Nicolae Dragos
- concurs
- Clasa 10 Structuri de date liniare Coada
- Algoritmul lui Lee
#629
Zet
Fie \(z \in R, z \neq 0\) astfel încât \(z + \frac{1}{z} = k, k \in N\).
Dându-se k și un număr natural n, se cere:
a) să calculați \(z^2 + \frac{1}{z^2}\) ;
b) să se determine \(z^n + \frac{1}{z^n}\) .
Grigore Moisil, 2014
- Fișiere
- concurs
- Clasa 10 Probleme diverse Diverse
#626
Anagrame2
Călin a primit de la învățătorul lui un exerciţiu pentru a-i testa atenția și rapiditatea. Având un șir de caractere, litere ale alfabetului englez și un cuvânt, Călin trebuie să afle care este prima anagramă (un cuvânt c1 este anagramă pentru alt cuvânt c2 dacă schimbând ordinea literelor lui c1 se obține c2) a cuvântului în șir și câte anagrame sunt. Călin, fiind pasionat de informatică dorește să rezolve această problemă printr-un program.
Cunoscând șirul de caractere și cuvântul se cere:
a) să se afișeze prima anagramă a cuvântului în șir;
b) câte anagrame ale cuvântului sunt.
Grigore Moisil, 2014
- Fișiere
- Serban Alexandru Florian
- concurs
- Clasa 10 Şiruri de caractere Probleme diverse
#625
vraji
Harry se află într-un duel de vrăjitori și vrea să folosească cea mai puternică vrajă pe care și-o amintește în acest moment. Deoarece mai devreme a fost lovit de o vrajă a uitării, are nevoie de ajutorul vostru pentru a calcula rapid cea mai puternică vrajă dintr-un set de vrăji. Vrăjile sunt șiruri de caractere, litere mici ale alfabetului englez, fară spații între ele.
Exemple: stupefy, accio, expelliarmus, depulso, levicorpus, reductuu, coooptuus etc.
Puterea unei vrăji se calculează în funcție de numărul de vocale și de consoane pe care le are vraja, după formula: [(nrv*V+nrc*C)/nrd]+1, unde:
V– puterea unei vocale;C– puterea unei consoane;nrv– numărul de vocale din vrajă;nrc– numărul de consoane din vrajă;nrd– numărul de litere distincte din vrajă;[a]– reprezintă partea întreagă a numărului a.
Se vor considera vocale: a, e, i, o, u, q, w, y.
Se numeşte grup o secvenţă de cel puţin două litere identice. Un grup se numeşte maximal, dacă este delimitat de litere diferite de conţinutul său, respectiv de începutul sau sfârşitul vrăjii.
Spre exemplu: în vraja coooptuus, ooo și uu sunt grupuri maximale, însă oo nu este grup maximal.
Deoarece Harry este un vrăjitor special, acesta are abilitatea de a calcula puterea fiecărui grup maximal dintr-o vrajă, și apoi să o adune la puterea acesteia. Puterea unui grup se obține înmulțind puterea literei respective cu ea însăși de același număr de ori câte litere identice are grupul.
Exemple: pentru V=5 și C=2, stupefy are puterea [(3*5+4*2)/7)]+1=3+1=4;
accio are puterea [(3*5+2*2)/4]+1+2*2=4+1+4=9;
reductuu are puterea [(4*5+4*2)/6]+1+5*5=4+1+25=30.
După lovitura primită, Harry mai știe doar N vrăji.
Se numește vrajă specială o vrajă pe care Harry își poate folosi abilitatea specială.
Exemple: accio și reductuu sunt vrăji speciale, deoarece au fiecare cel puțin un grup maximal de două litere identice;
stupefy nu este o vrajă specială deoarece nu are are niciun grup de litere identice.
Cunoscând N, V, C și vrăjile pe care le mai știe Harry, se cere:
a)numărul total de vrăji speciale;
b)prima vrajă de putere maximă pe care Harry şi-o aminteşte, și câte astfel de vrăji poate folosi eroul nostru.
Grigore Moisil, 2014
- Fișiere
- concurs
- Clasa 10 Şiruri de caractere Probleme diverse
#630
Joc
Mihai, fiind un mare pasionat al jocurilor în aer liber, a inventat un joc nou în speranța că își va convinge colegii să iasă afară să se joace. Jocul lui Mihai spune că se dau N pătrate ce se află la anumite nivele iar din fiecare pătrat se poate sări doar în anumite pătrate stabilite la începutul jocului. Dacă un jucător sare dintr-un pătrat aflat la nivelul X într-un pătrat aflat la un nivel mai mare Y, acesta folosește un efort egal cu [Y/X], iar dacă sare într-un pătrat aflat la un nivel mai mic sau egal Y, efortul folosit este [X/Y]. Jucătorul se află la început în pătratul de start S și scopul jocului este să ajungă în pătratul final F, depunând un efort minim.
Cunoscând numărul de pătrate N, pătratul de start S, pătratul final F și pentru fiecare pătrat, pătratele în care jucătorul poate sări, se cere:
a) Efortul minim necesar pentru a ajunge în pătratul final.
b) Pătratele pe care jucătorul le sare până ajunge la pătratul final.
Grigore Moisil, 2014
- Fișiere
- Serban Alexandru Florian
- concurs
- Clasa 11 Teoria Grafurilor Grafuri cu costuri
- Algoritmul lui Dijkstra
#631
Passwd
Alexandru dorește să devină expert în securitate, iar pentru aceasta s-a apucat să învete mai multe despre siguranța parolelor. El dorește să afle câte parole poate crea folosind a litere mici ale alfabetului englez și b litere mari ale alfabetului englez, c cifre si d caractere din mulțimea {!, @, #, $, %}. Totodată, el vrea să găsească parola cu numărul x în ordine lexicografică, formată din caracterele descrise mai sus.
Cunoscând a, b, c, d si x se cere:
a) A x-a parolă în ordine lexicografică, formată din caracterele menționate în enunț.
b) Numărul de parole diferite formate din caracterele menționate în enunț, modulo 666013.
Grigore Moisil, 2014
- Fișiere
- Nicolae Dragos
- concurs
- Clasa 11 Probleme diverse Probleme diverse