Lista de probleme 78

Un fermier are un teren care are forma unui tablou dreptunghiular de N x M unități. Pe teren sunt plantați din loc în loc copaci, pe care fermierul nu dorește sa-i taie. Dorind să-și supravegheze cultura, fermierul realizează un mic robot de forma pătrată având latura de 3 unități pe care îl poate teleghida prin fermă, parcurgând unitate cu unitate o anumită suprafață. Robotul se poate mișca pe verticală și pe orizontală dar nu poate trece peste copaci, nu îi poate distruge, nu se poate roti și are nevoie pentru mișcare de o suprafață corespunzătoare dimensiunii lui. Ajutați-l pe fermier sa determine suprafața maxima pe care o poate urmări, folosind acest sistem.

Arheologii au descoperit pe un platou muntos greu accesibil ruinele unui castel medieval, pe care l-au fotografiat din elicopter, obţinând harta digitizată a acestuia. Harta este memorată sub forma unui tablou bidimensional H, compus din N x N pătrate cu latura egală cu unitatea, având ca elemente numere naturale între 0 și 15, care codifică forma pereţilor fiecărui pătrat unitar. Dacă scriem numărul natural H[i][j] în baza 2, folosind exact 4 cifre binare, fiecare bit dă informații despre unul dintre pereții posibil de construit pe fiecare latură a pătratului unitar din poziția (i,j), astfel:

• dacă bitul de pe poziția 0 are valoarea 1, atunci există perete pe latura vestică (latura din stânga);
• dacă bitul de pe poziția 1 are valoarea 1, atunci există perete pe latura sudică (latura de jos);
• dacă bitul de pe poziția 2 are valoarea 1, atunci există perete pe latura estică (latura din dreapta);
• dacă bitul de pe poziția 3 are valoarea 1, atunci există perete pe latura nordică (latura de sus);
• un bit de valoare 0 indică lipsa peretelui corespunzător acestuia;

Pentru un număr scris în baza 2, numerotarea cifrelor începe cu poziția 0, de la dreapta la stânga.
Castelul este interesant deoarece, pentru realizarea unei mai bune apărări, camerele ce-l compun sunt construite fie independent, fie una în interiorul alteia. Orice camera este construită la o distanţă de cel puţin o unitate faţă de zidul ce împrejmuieşte castelul sau faţă de pereţii altor camere.
Folosind harta, arheologii doresc să afle informaţii privind numărul camerelor şi camera de arie maximă. Prin arie a unei camere se înţelege numărul pătratelor unitate cuprinse în interiorul pereților aceasteia, fără a socoti ariile camerelor construite în interiorul ei.

Cunoscând codificarea hărţii castelului, să se determine:
1. numărul total al camerelor din castel
2. aria maximă a unei camere
3. coordonatele colţurilor din stânga-sus, respectiv dreapta-jos a camerei cu aria maximă. Dacă există mai multe camere având aceeaşi arie maximă, atunci se vor afişa coordonatele camerei având colţul din stânga-sus (lin1, col1) cu lin1 minimă, iar la linii egale pe aceea cu col1 minimă.

Fetiţele şi băieţii Powerpraff s-au aşezat într-un şir s de lungime K, ei fiind reprezentaţi în şir prin caracterele f şi b. Cum până la apariţia noilor episoade s-a descoperit şi clonarea, acest şir a fost multiplicat de N ori, iar şirul nou obţinut, de lungime N x K, se aşează în ordine, pe linii de câte D caractere. Doi băieţi sunt prieteni dacă se învecinează pe orizontală sau verticală în noua aşezare pe linii. Doi băieţi Bx şi By sunt în aceeaşi gaşcă dacă sunt prieteni sau dacă există un şir de băieţi B1, B2, …, Bm (eventual m poate fi şi 0) astfel încât în şirul Bx, B1, B2, …, Bm, By oricare doi băieţi alăturaţi sunt prieteni. O gaşcă poate fi formată din cel puţin un băiat. Cunoscând valorile lui K, N şi D, precum şi caracterele din şirul s, aflaţi numărul de găşti care se pot forma, ştiind că fiecare băiat face parte dintr-o singură gaşcă.

Vi se dă un număr natural n și o secvență b[1], ..., b[n] ∊ {true, false}. Se garantează că există un număr natural k pentru care n = 2k - 1. Trebuie să generați o permutare p a elementelor {1, 2, ..., n} care îndeplinește anumite condiții. Fie S(p) numărul de indici i ∈ {1, 2, ..., n} pentru care binary_search(n, p, i) nu returnează b[i].

Satul Binăreni se află în pericol în urma incendiilor provocate în ultima lună. Acesta este reprezentat printr-o matrice binară cu N linii și M coloane. Toate celulele care au luat foc sunt reprezentate prin valoarea 0. Toate celulele în care nu este produs un incendiu, reprezentate prin valori de 1, conțin, inițial, câte o casă a unui sătean. Gosu, cel mai renumit pompier din sat, își dorește să salveze toate casele care nu se află în celule "safe", folosindu-și superputerea: acesta poate stinge o singură dată focul din toate celulele care au luat foc pe o linie x și toate celulele care au luat foc pe o coloană y, plasându-se la intersecția acestora, în celula (x, y). Acesta se poate plasa atât pe o celulă cu incendiu, cât și pe o celulă care conține o casă. Având în vedere că Gosu își poate folosi superputerea o singură dată, aflați toate perechile de coordonate (x, y) posibile pe care se poate plasa acesta, astfel încât să salveze toate casele care sunt în pericol.

În Tărâmul Magic al Insulelor, se desfășoară o vânătoare anuală de comori, unde echipele explorează insule fermecate, delimitate de apa ce le înconjoară. La ordinul regelui A., sunt ascunse comori pe fiecare insulă. Harta tărâmului este reprezentată sub forma unei matrice de dimensiune 𝑛 × 𝑚, ale cărei elemente codifică zone pătratice, cu latura de 1 metru. Acestea pot fi:

• zonă care conține apă, marcată cu −1;
• zonă care conține doar pământ, marcată cu 0; sau
• zonă care conține pământ și o singură comoară, marcată cu un număr natural nenul.

Două zone se consideră vecine dacă au o latură comună. Două zone aparţin aceleiaşi insule dacă ele sunt vecine sau dacă se poate ajunge de la o zonă la cealaltă pe un drum care parcurge o succesiune de zone, oricare două zone parcurse consecutiv fiind vecine. În acest an, căpitanul Poseidon dorește să facă o farsă regelui A., permutând comorile, astfel încât fiecare comoară să fie mutată într-o zona în care inițial a fost o altă comoară. Totuși, pentru a nu atrage atenția prea mult, comorile vor rămâne în cadrul insulei pe care se aflau inițial

Pentru început, căpitanul Poseidon își propune să rezolve următoarele cerințe:

1. Câte comori se găsesc pe insula pe care se află căpitanul Poseidon?
2. Câte soluții există pentru plasarea tuturor comorilor, astfel încât fiecare comoară să fie mutată în cadrul aceleiași insule, într-o zonă în care inițial a fost o altă comoară? Pentru că numărul de soluții poate fi foarte mare, răspunsul va fi afișat modulo 1 000 000 007.

Privit din satelit, Golful Biscayne (Florida) este format din n × m celule pătratice, fiecare celulă fiind umplută fie cu pământ, fie cu apă. Celulele umplute cu pământ sunt grupate în insule: două celule umplute cu pământ fac parte din aceeași insulă dacă și numai dacă se poate ajunge de la una la cealaltă prin deplasare (în sus, jos, stânga sau dreapta) doar pe pământ.

Golful poate fi văzut, astfel, ca o matrice A cu n linii și m coloane (numerotate de la 1), unde A[i][j] = 1 dacă celula de pe linia i și coloana j este umplută cu pământ și A[i][j] = 0 dacă este umplută cu apă.

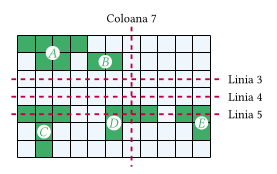
Spunem că o insulă se află la stânga unei coloane c dacă și numai dacă toate celulele ce intră în alcătuirea insulei sunt strict la stânga coloanei c, adică sunt situate pe coloane strict mai mici decât c. Analog, stabilim dacă o insulă se află la dreapta unei coloane c, respectiv deasupra sau dedesubtul unei linii l. De exemplu, în desenul de mai sus, insulele A, B și C sunt la stânga coloanei 7, insula E este la dreapta coloanei 7, iar insula D nu este nici la stânga, nici la dreapta coloanei 7. De asemenea, insulele A și B sunt deasupra liniei 3, iar insulele C, D și E sunt dedesubtul liniei 4. Mai mult, insulele C, D și E nu sunt nici deasupra, nici dedesubtul liniei 5.

Problema are trei cerințe, cerința de rezolvat fiind dată de T ∈ {1, 2, 3}.

• T = 1. Determinați numărul de celule din golf ce sunt umplute cu pământ.
• T = 2. Determinați numărul de insule din golf ce conțin un număr maxim de celule. Dacă nu există nicio insulă, atunci valoarea acestui număr este 0.
• T = 3. Se dau, în ordine, Q interogări, fiecare fiind descrisă printr-o literă și un număr natural
  nenul p. Determinați valoarea produsului a × b, știind că:
  • Dacă litera este C, atunci a reprezintă numărul de celule din toate insulele ce se află la stânga coloanei p (1 ≤ p ≤ m) și b numărul de celule din toate insulele ce se află la dreapta coloanei p.
  • Dacă litera este L, atunci a reprezintă numărul de celule din toate insulele ce se află deasupra liniei p (1 ≤ p ≤ n) și b numărul de celule din toate insulele ce se află dedesubtul liniei p.

Pentru a îmbunătăţi aptitudinile logico-matematice ale elevilor săi, profesorul Vasile a implementat un joc. Pe ecranul principal al jocului se afişează un şir de N scaune, numerotate de la stânga spre dreapta începând cu 1, pe fiecare scaun fiind așezat câte un copil. Fiecare copil poartă un tricou pe care este scris, de asemenea, câte un număr de la 1 la N. Numerele de pe tricouri sunt distincte și sunt scrise pe spate, deci nu sunt vizibile. Scopul jocului este de a descoperi numărul scris pe tricoul fiecărui copil. Pentru aceasta, pe ecran mai este afişat un triunghi de numere T, care ne dă informaţii ajutătoare. Triunghiul arată ca o matrice în care liniile sunt numerotate de sus în jos de la 1 la N, iar coloanele de la stânga la dreapta de la 1 la N. Numărul scris în triunghi pe linia i şi coloana j (1 ≤ i ≤ j ≤ n) reprezintă numărul scaunului pe care stă copilul având cel mai mic număr pe tricou dintre toţi copiii situaţi pe scaune cu numere cuprinse între i şi j (inclusiv i şi j). Observaţi că poziţiile din triunghi de pe linia i şi coloana j cu 1 ≤ j < i ≤ N nu sunt completate. Cunoscând numărul de copii şi triunghiul de numere:
1. determinați o soluţie posibilă; dacă există mai multe soluţii posibile se va afişa cea mai mică din punctul de vedere lexicografic;
2. determinați numărul de soluţii posibile.