Lista de probleme 82
Filtrare
fmat
#3363
Fie o matrice (care are M linii si N coloane) colorată folosind C culori. Aceasta este K-frumoasă doar dacă are exact K coloane omogene. O coloană omogenă este o coloană care are toate elementele colorate la fel.
Clasa0
#3853
Astăzi în clasa 0 profesoara a numit Q copii și le-a dat 3 numere, a, b și c, copiii trebuiau să spună care este rezultatul calculului
CsAcademy
Spion1
#1110
Spionul 008 vrea să găsească o locație secretă în junglă, având asupra lui un dispozitiv de localizare. Iniţial spionul se află la intrarea în junglă pe nivelul 1 şi cu fiecare pas, el avansează de la nivelul i la nivelul i+1, ajungând la locaţia secretă, aflată pe ultimul nivel, în poziţia u faţă de marginea stângă a nivelului curent. Pentru a ajunge în locaţia secretă, el poate să se deplaseze cu o poziţie spre Sud-Est (codificat cu caracterul E) sau spre Sud-Vest (codificat cu caracterul V), trecând de pe nivelul i pe nivelul i+1 cu viteză constantă. Numărul de poziţii de pe un nivel creşte cu unu faţă de nivelul anterior, conform imaginii alăturate. Numim traseu o succesiune formată din caracterele E sau V, corespunzătoare deplasării spionului de pe nivelul 1 la locaţia secretă. Pentru exemplul din figura alăturată succesiunea de caractere VEEVE reprezintă un traseu ce corespunde locaţiei secrete din poziţia 4 a nivelului 6.
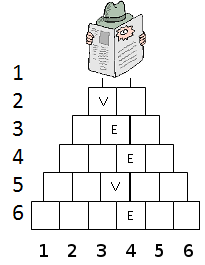
Cunoscând succesiunea de caractere corespunzătoare unui traseu, determinaţi:
a) poziţia locației secrete de pe ultimul nivel;
b) numărul de trasee distincte pe care le poate urma spionul plecând din poziţia inițială pentru a ajunge în locaţia secretă corespunzătoare traseului dat. Două trasee se consideră distincte dacă diferă prin cel puţin o poziţie.
ONI 2014, Clasa a X-a
Expozitie
#1091
Ilinca este o fetiţă căreia îi place foarte mult să deseneze; ea a făcut multe desene pe care le-a numerotat de la 1 la d şi apoi le-a multiplicat (toate copiile poartă acelaşi număr ca şi originalul după care au fost făcute). În vacanţă s-a hotărât să-şi deschidă propria expoziţie pe gardul bunicilor care are mai multe scânduri; pe fiecare scândură ea aşează o planşă (un desen original sau o copie). Ilinca ţine foarte mult la desenele ei şi doreşte ca fiecare desen să apară de cel puţin k ori (folosind originalul şi copiile acestuia). Ilinca se întreabă în câte moduri ar putea aranja expoziţia. Două moduri de aranjare sunt considerate distincte dacă diferă cel puţin prin numărul unei planşe (de exemplu: 2 1 3 3 este aceeaşi expoziţie ca şi 2 3 1 3, dar este diferită de 2 1 3 1 şi de 1 3 3 1).
Cunoscând n numărul de scânduri din gard, d numărul desenelor originale şi k numărul minim de apariţii al fiecărui desen, să se determine în câte moduri poate fi aranjată expoziţia, ştiind că Ilinca are la dispoziţie oricâte copii doreşte.
OJI 2010, Clasa a X-a
Cifru
#722
Alibaba trebuie să descopere cifrul care deschide cufărul cu comoara cea mare. Cifrul este foarte greu de găsit. El a descoperit mai multe pietre, fiecare piatră având o altă culoare, pe fiecare piatră fiind scris un număr natural cu cel mult 4 cifre. Alibaba observă că numerele de pe fiecare piatră sunt distincte două câte două. Regula după care se formează cifrul este una foarte simplă, şi Alibaba a reuşit să o obţină destul de uşor: cifrul este format din alăturarea într-o anumită ordine a tuturor pietrelor. Ceea ce Alibaba mai ştie este că pe poziţia p din cifru se găseşte cu siguranţă cifra k.
Scrieţi un program care determină numărul de variante de cifruri pe care va trebui să le încerce Alibaba. Numărul fiind foarte mare se va calcula modulo 46337.
Lot Juniori, Focsani, 2010
Implementare
#717
Se consideră algoritmul:
citeşte k , n;
s = 0;
for (i1 = 1 ; i1 ≤ k ; i1++)
for (i2 = 1 ; i2 ≤ i1 ; i2++)
for (i3 = 1 ; i3 ≤ i2 ; i3++)
........................................
for (in = 1 ; in ≤ in-1 ; in++)
s = s + in;
scrie s;
stop.
Să se scrie un program care implementează algoritmul de mai sus.
Lot Juniori, Resita, 2012
SumAll
#695
Fie N un număr natural format din cifre nenule.
Să se determine suma tuturor numerelor distincte ce se pot forma cu toate cifrele numărului N.
Lot Juniori, Sovata, 2014
calatorie
#679
Dorești să mergi în vacanță și ai hotărât deja destinația. Formal, te afli în punctul (0,0) al unui sistem cartezian de axe și trebuie să ajungi în punctul de coordonate (X,X). Țara în care te afli are drumuri paralele cu axele de coordonate la fiecare abscisă și la fiecare ordonată număr natural. În fiecare moment, dacă eşti în punctul de coordonate (a,b), ai 2 variante de deplasare: în punctul (a,b+1) sau în punctul (a+1,b). La fiecare astfel de pas consumi un litru de carburant. Prin unele puncte de forma (a,a) nu poți trece, iar în celelalte puncte care au abscisa egală cu ordonata poți trece și în plus, acolo se află câte o stație de benzină unde poți să „faci plinul”. Prin toate punctele care nu au abscisa egală cu ordonata poți trece dar acolo nu se află stații de benzină. Rezervorul mașinii tale are o capacitate de K litri.
Determinați numărul de trasee distincte prin care poți ajunge la destinație. Două trasee sunt distincte dacă diferă prin cel puţin un punct.
Lot Juniori, Vaslui, 2014
kswap
#1232
Fie A = (a[1],a[2],…,a[N]) o permutare a mulțimii {1,2,…,N}.
Permutarea A o numim K-swap dacă prin aplicarea algoritmului de sortare bubble-sort sunt necesare exact K swapuri (interschimbări) pentru ca aceasta să devină permutarea identică.
Reamintim algoritmul bubble-sort:
do { ok = 1; for ( i = 1; i < N; i ++ ) if ( a[i] > a[i+1] ){ swap(a[i], a[i+1]); ok = 0; } }while( ok == 0 );
Pentru N și K dat să se determine numărul de permutări K-swap ale mulțimii {1,2,…,N}.
Lot Juniori, Valcea, 2015
Pastile
#1236
Manole este extrem de răcit. Din această cauză a mers la medicul de familie care l-a sfătuit urmeze un tratament cu N pastile, din care trebuie să ia în fiecare zi câte o jumătate. A cumpărat de la farmacie o cutie în care se aflau exact N pastile, fiecare dintre ele având pe suprafață o dungă care marchează jumătatea ei.
Manole începe să își ia tratamentul și constată că poate proceda doar astfel:
- scoate din cutie o pastilă întreagă din care folosește, în ziua respectivă, doar jumătate din ea, iar jumătatea rămasă o pune înapoi în cutie;
- scoate din cutie o jumătate de pastilă, rămasă din una din zilele anterioare, pe care o folosește în ziua respectivă.
Scrieți un program care determină numărul de posibilități în care poate lua toate cele N pastile, procedând după procedeul descris mai sus.
Lot Juniori, Valcea, 2015